4sin^3 x +3 sinx+4√3=4√3 cos^2 x
решить,задание из егэ
Ответы
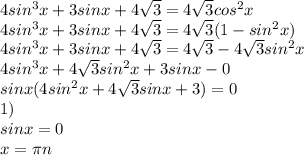 ; n ∈ Z
; n ∈ Z
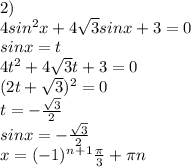 ; n ∈ Z
; n ∈ Z
Другие вопросы по теме Математика
Популярные вопросы
- Как вратарь отбивает мячи , летящие в ворота?...
2 - Преобразовать выражение: (-12)*(-х-у+2)...
3 - Нарисуй круг радиусом 3 клетки перенеси его на 9 клеток нет потом на...
3 - Вкаких произведениях человек лишался памяти?...
3 - Напиши текст по плану: 1)где живёт лось? 2)почему его называют лесным...
3 - Як ви розумієте вислів слово чужинцям кинуте на сміх, співочий грім...
2 - Гамлет. 1.кто из героев раскрывает коварность розенкранца и гильденстерна?...
2 - Детский бассейн ёмкостью 921 л заливается водой с двух труб одновременно....
2 - Прямолинейный проводник длиной 1,5 м находимся в однородном магнитном...
3 - )какое место в советской внешней политике занимал коммунистический интернационал...
3