42 певца записывают песню, в которой есть несколько куплетов и припевов в определенном порядке. Каждый куплет поется ровно
6 певцами, а каждый припев — ровно 4 певцами. Каждый певец
может спеть только в одном куплете или припеве, в песне есть хотя
бы один куплет и хотя бы один припев, два куплета не идут сразу друг
после друга, никакой припев не может быть одновременно до и после
припевов. Необязательно использовать всех певцов для записи. Сколько
различных количеств певцов нужно для исполнения таких песен?
Распишите поподробней решение .

Ответы

Лино444ка 29.08.2021 14:10

Разберем структуру песни. Обозначим куплет как К, а припев как П.

Пусть в песне есть k куплетов:

$K_1\ K_2\ K_3\ \ldots\ K_k$

По условию, между куплетами может стоять 1 или 2 припева, а до первого и после последнего куплета - 0, 1 или 2 припева:

$\left(\begin{array}{c}\times\\\Pi\\\Pi\Pi\end{array}\right) K_1\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) K_2\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) K_3\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) \ldots\ K_k\left(\begin{array}{c}\times\\\Pi\\\Pi\Pi\end{array}\right)$

Определим минимальное и максимальное возможное число припевов для k куплетов.

Минимальное число припевов соответствует случаю, когда между всеми куплетами стоит по одному припеву, а припевы до первого куплета и после последнего куплета отсутствуют. Так как промежутков между k куплетами (k-1), то этому же числу и равняется минимальное число припевов:

$\Pi_{\min}=k-1$

Заметим, что для одного куплета формула даст число припевов, равное нулю. Но по условию в песне есть хотя бы один припев. Тогда можно записать:

$\Pi_{\min}=\max(k-1;\ 1)$

Максимальное число припевов соответствует случаю, когда между всеми куплетами стоит по два припева, а также до первого куплета и после последнего куплета стоит по два припева. Тогда, максимальное число припевов:

$\Pi_{\max}=2(k-1)+2+2=2k-2+2+2=2k+2$

Рассмотрим песни с одним куплетом.

k=1

Тогда:

$\Pi_{\min}=1$

$\Pi_{\max}=2\cdot1+2=4$

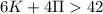Введем функцию $f(K;\ \Pi)=6K+4\Pi$ , позволяющую по числу куплетов и припевов находить нужно число певцов. Можно ввести ограничение, например, о том, что при $6K+4\Pi42$ - функция не определена, так как по условию имеется 42 певца.