1. Математика
  2. 40 , ! найти площадь фигуры, ограниченной

40 , ! найти площадь фигуры, ограниченной линиями и объём тела, полученного вращением этой фигуры вокруг оси ox у=х² - 2x +2 , y=0, x=-1, x=2

Anna888Anna1 Anna888Anna1    3   14.08.2019 15:30    2

Ответы
Alina29521 Alina29521  04.10.2020 19:03
Y=x²-2x+2,y=0,x=-1,x=2
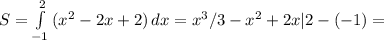
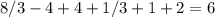
S= \int\limits^2_{-1} {(x^2-2x+2)} \, dx =x^3/3-x^2+2x|2-(-1)=8/3-4+4+1/3+1+2=6
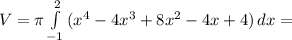
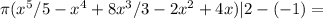
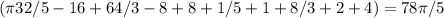
V= \pi \int\limits^2_{-1} {(x^4-4x^3+8x^2-4x+4)} \, dx =\pi (x^5/5-x^4+8x^3/3-2x^2+4x)|2-(-1)=( \pi 32/5-16+64/3-8+8+1/5+1+8/3+2+4)=78 \pi /5
ПОКАЗАТЬ ОТВЕТЫ
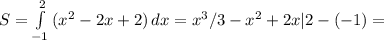
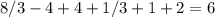
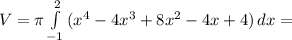
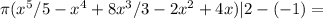
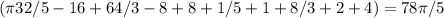
Другие вопросы по теме Математика
iroytblatилья iroytblatилья  28.10.2020 16:42
Не просто ответ нет, да, а полностью действия с объяснением ​...
necoshevcom necoshevcom  28.10.2020 16:42
Решите нужны чертежи, дано ,найти, решение, или же дано доказать,доказательство. решите правильно...
Бобер3009 Бобер3009  28.10.2020 16:42
Дан угол MON и точка K, не лежащая в его внутренней области. А) постройте луч KD , который пересекал бы луи OM и ON; Б) постройте развернутый угол KOP; В) Какие из точек M,...
елка12345 елка12345  28.10.2020 16:42
70 метров в квадрате минус 43 метров в квадрате​...
Asel272727 Asel272727  28.10.2020 16:42
Найдите значение вызажения: 5/8×|0,8|+|-4,5|:0,3​...
kravchenkoev kravchenkoev  28.10.2020 16:42
Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Желательно с графиком...
okolota05 okolota05  28.10.2020 16:42
Сравни значення величин.2 км 800 м8 см 4 мм84 мм2 м 21 дм6 дм 3 см 549мм​...
olyakak00Fokcu olyakak00Fokcu  28.10.2020 16:42
419. Числа 2, 4, 9, 10 и 26 запишите в виде смешанного числа со знаменателем 7.Например. Запишем число 8 в виде смешанного числа сознаменателем 3.​...
ЗалияАлиматова ЗалияАлиматова  28.10.2020 16:42
Не понимаю, что я делаю не так, коэффициент подобия 2 же, но правильный ответ 13...
berfasrd berfasrd  28.10.2020 16:42
Может ли модуль числа быть отрицательным числом? (в ответе указать да или нет)...

Популярные вопросы