1. Математика
  2. 4^x-4^y=6, 4^(x+y)=16

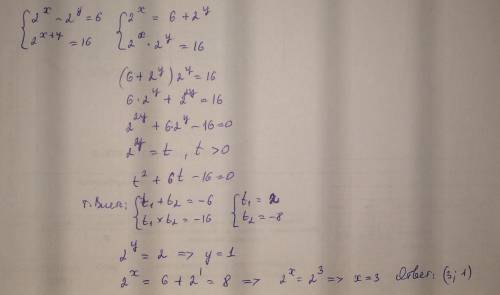
4^x-4^y=6, 4^(x+y)=16 система уравнений Решить нужно есть пример ниже


4^x-4^y=6, 4^(x+y)=16 система уравнений Решить нужно есть пример ниже

whitesnaff whitesnaff    2   26.06.2020 22:29    1

Ответы
NastiaZaic NastiaZaic  15.10.2020 14:59

\left \{ {{x=\frac{3}{2} } \atop {y\\=\frac{1}{2} }} \right.

Пошаговое объяснение:

4^{x+y}=16 = 4^{x+y}=4^2 = x+y=2

4^x - 4^y=6 = 4^x-4^{2-x}=6 = 4^x-\frac{4^2}{4^x} =6 Умножаем все на 4^x

получаем

4^{2x} -4^2=6*4^x = 4^{2x}-6*4^x -16=0

заменяем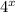 4^x на новую переменную t, где t>0

получаем

t^2-6t-16=0

решаем простейшее квадратное уравнение

получаем t={8;-2},

-2 выкидываем т.к t>0

4^x=t = 4^x=8 = x=log_{4}8 = x=\frac{1}{2} log_{2}8 = x=\frac{3}{2}

далее без труда находим y

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
roman81rudi roman81rudi  08.09.2019 01:10
Почему бездуховность человека принято считать одной из причин правонарушений?...
данил1234758888 данил1234758888  08.09.2019 01:10
Вклассе учились 10 девочек и столько же мальчиков. когда пришло ещё несколько человек, их стало 25. сколько человек пришли в класс?...
Hitecho07 Hitecho07  08.09.2019 01:10
Запишите дроби 7/8 5/12 9/16 в порядке убывания, а дроби 5/6 7/10 13/15 в порядке возрастания...
RILIR RILIR  08.09.2019 01:10
Чему равен наименьший делитель если при делении получится остаток 4 какой остаток получится если 27 / 4...
14sanka 14sanka  08.09.2019 01:10
Технология 7 класс, что значит сг п в мерках по платью и как это мерить?...
sashaboyko999p089tm sashaboyko999p089tm  08.09.2019 01:10
Известо, что с полным баком топлива рыбак проплывает на моторной лодке 30 км по течению или 20 км против течения реки. на какое наибольшее расстояние может отплыть рыбак по реке...
PavelSahka PavelSahka  08.09.2019 01:10
Аесли нок (12; 14; 42) а 14 и 12 не делится на 84...
алиса673 алиса673  08.09.2019 01:10
Рассказать о природных катаклизмах связанных с литосферой...
sanik98 sanik98  08.09.2019 01:10
Краткий доклад памятники превобытности...
timurtim1 timurtim1  08.09.2019 01:20
Нужно составить текст качество друга по этике про машу...

Популярные вопросы