4) Выполните задания. Удалите неправильные варианты ответов.

Оставьте в колонке только правильные ответы.

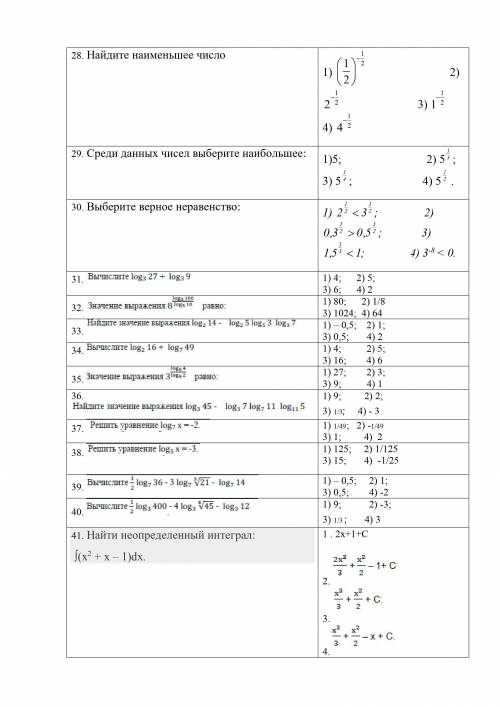
4) Выполните задания. Удалите неправильные варианты ответов. Оставьте в колонке только правильные от

Ответы

Yan132142 13.02.2021 20:16

28. 4

29. 1

30. 1

31. 2

32. 4

33. 2

34. 4

35. 3

36. 2

37. 1

38. 2

39. 4

40. 2

41. 4

Пошаговое объяснение:

28.

${( \frac{1}{2}) }^{ - \frac{1}{2} } = \sqrt{2} = 1.4 \\ {2}^{ - \frac{1}{2} } = \frac{1}{ \sqrt{2} } = \frac{1}{1.4} = \frac{10}{14} = \frac{5}{7} \\ {1}^{ - \frac{1}{2} } = 1 \\ {4}^{ - \frac{1}{2} } = \frac{1}{ \sqrt{4} } = \frac{1}{2} = 0.5$

вывод: чем больше основание при отрицательной степени, тем меньше число

29.

для этого сравним степени:

$1 \frac{1}{2} \frac{1}{3} \frac{1}{4} \\$

больше 5 в первой степени

30.

степени одинаковые, сравним основания

1)2 < 3

верное неравенство

$2)0.3 < 0.5 \: \: = \: \: {(0.3)}^{ \frac{1}{2} } < {(0.5)}^{ \frac{1}{2} } \\$

неверное неравенство

$3)1 = {1}^{ \frac{1}{3} } \\ {1.5}^{ \frac{1}{3} } {1}^{ \frac{1}{3} }$

неверно

$4) {3}^{ - 8} = \frac{1}{ {3}^{8} } 0 \\$

неверное

ответ: верное 1)

31.

$log_{3}(27) + log_{3}(9) = log_{3}(27 \times 9) = \\ = log_{3}( {3}^{3} \times {3}^{2} ) = log_{3}( {3}^{5} ) = 5$

32.

${8}^{ \frac{ log_{3}(100) }{ log_{3}(10) } } = {8}^{ log_{10}(100) } = {8}^{2} = 64 \\$

33.

$log_{2}(14) - log_{2}(5) log_{5}(3) log_{3}(7) = \\ = log_{2}(14) - \frac{ log_{5}(3) }{ log_{5}(2) } log_{3}(7) = \\ = log_{2}(14) - log_{2}(3) log_{3}(7) = \\ = log_{2}(14) - \frac{ log_{3}(7) }{ log_{3}(2) } = \\ = log_{2}(14) - log_{2}(7) = log_{2}( \frac{14}{7} ) = \\ = log_{2}(2) = 1$

34.

$log_{2}(16) + log_{7}(49) = 4 + 2 = 6$

35.

${3}^{ \frac{ log_{5}(4) }{ log_{5}(2) } } = {3}^{ log_{2}(4) } = {3}^{2} = 9$

36.

$log_{3}(45) - log_{3}(7) log_{7}(11) log_{11}(5) = \\ = log_{3}(45) - log_{3}(7) \times \frac{ log_{11}(5) }{ log_{11}(7) } = \\ = log_{3}(45) - log_{3}(7) log_{7}(5) = \\ = log_{3}(45) - \frac{ log_{7}(5) }{ log_{7}(3) } = \\ = log_{3}(45) - log_{3}(5) = \\ = log_{3}( \frac{45}{5} ) = log_{3}(9) = 2$

37.

$log_{7}(x) = - 2 \\ x = {7}^{ - 2} \\ x = \frac{1}{49}$

38.

$log_{5}(x) = - 3 \\ x = {5}^{ - 3} = \frac{1}{125}$

39.

$\frac{1}{2} log_{7}(36) - 3 log_{7}( \sqrt[3]{21} ) - log_{7}(14) = \\ = log_{7}( \frac{ {36}^{ \frac{1}{2} } }{ {( \sqrt[3]{21} )}^{3} \times 14} ) = log_{7}( \frac{6}{21 \times 14} ) = \\ = log_{7}( \frac{1}{7 \times 7} ) = - 2$

40.

$\frac{1}{2} log_{3}(400) - 4 log_{3}( \sqrt[4]{45} ) - log_{3}(12) = \\ = log_{3}( \frac{ {400}^{ \frac{1}{2} } }{ {( \sqrt[4]{45} )}^{2} \times 12 } ) = log_{3}( \frac{20}{45 \times 12} ) = \\ = log_{3}( \frac{1}{9 \times 3} ) = - 3$