4 Теорема Пифагора
полностью расписать

14

Пошаговое объяснение:

Пусть АВ = 4 , тогда

АВ^2 + AD^2 = BD^2

AD^2 = BD^2 - АВ^2

AD^2 = 25-16=9

AD = 3

P = AB + AD + CD + BC = 4+3+4+3 = 14

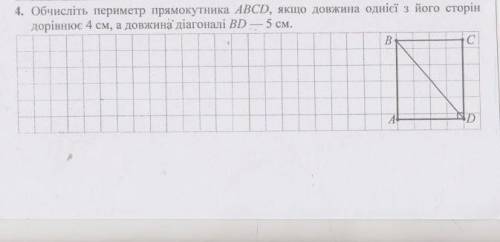
Дано: ABCD - прямоугольник

          BA = CD = 4 см

          BD = 5 см  

Найти: P abcd

Теорема Пифагора ⇒ с² = a² + b² ( гипотенуза в квадрате равна сумме квадратов катетов )

Диагональ BD делит прямоугольник ABCD на два одинаковых прямоугольных треугольника

Я буду рассматривать треугольник ABD , но можно решать и по треугольнику BCD.

AB и AD два катета, а BD является гипотенузой

Решаем по формуле  a² + b² = c², с которой находится гипотенуза прямоугольного треугольника , только немного изменим её чтобы можно было найти один из катетов  ⇒  a² = c² - b²

BA = b  ;  AD = a  ;  BD = c

AD² = BD² - BA²

AD² =  5² - 4²

AD² = 25 - 16

AD² =  9

AD = √9

AD = 3 см

Периметр прямоугольника находится по формуле   ⇒  P = 2 ( a + b ),

где a и b стороны прямоугольника

P abcd = 2 ( 4 + 3 ) = 2 · 7 = 14 см

ответ: Периметр прямоугольника равен 14 см