4. Сколько различных перестановок можно образовать из букв слова
«комбинаторика»?
Начало решения есть на фотографии
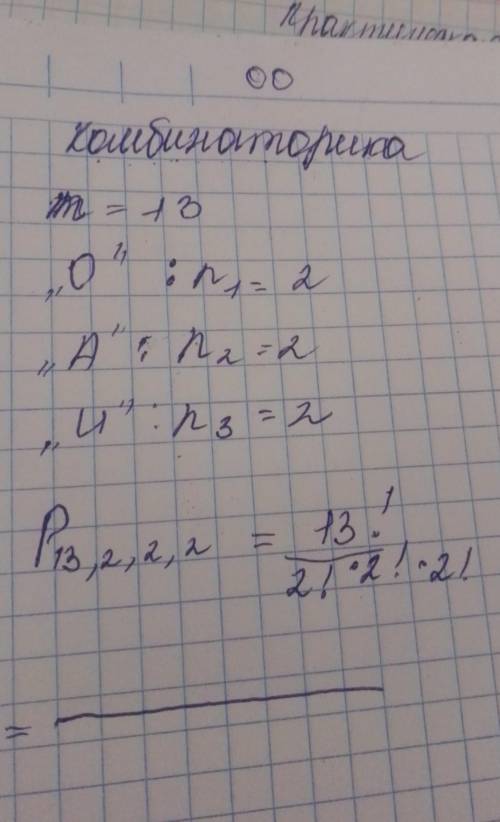
Другие вопросы по теме Математика
Популярные вопросы
- Кулики живут на болотах, по берегамкулики живут на болотах, по берегам рек,...
2 - Разбор слова камушкам? скажите нужно!...
3 - Всвязи с водным образом жизни у рыб появились следующие при...
2 - Переведите с языка на язык: 1)what have i /you /we/they got? 2)i have got...
2 - Сколько потребуется растений , чтобы в лесу вырос и мог существовать волк...
3 - Перевести на our flat is very large.there are three rooms in it we have...
3 - Рассмотрите фотографию инжира и характиристика...
1 - Сакские скотоводы в пустынных и полупустыных районах пасли...
3 - Вчем смысл произведения франсуаза саган ,грусть ?...
3 - Почему осенью бывает листопад? маленький текст....
2
По формуле перестановок с повторениями, общее число перестановок вычисляется по формуле:
P = n! / (n1! * n2! * ... * nk!)
где n - общее число объектов, n1, n2, ..., nk - числа повторяющихся элементов.
В данном случае, у нас есть слово "комбинаторика" с 13 буквами. Некоторые из этих букв повторяются, поэтому мы должны определить количество повторений для каждой буквы.
Посмотрев на фотографию, мы видим, что буква "о" повторяется 2 раза, буква "к" повторяется 2 раза, буква "и" повторяется 2 раза, а остальные буквы встречаются по одному разу.
Теперь мы можем подставить эти значения в формулу:
P = 13! / (2! * 2! * 2!)
Вычислим это значение:
P = (13 * 12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1) / ((2 * 1) * (2 * 1) * (2 * 1))
P = 6227020800 / 8
P = 778502600
Таким образом, из букв слова "комбинаторика" можно образовать 778 502 600 различных перестановок.