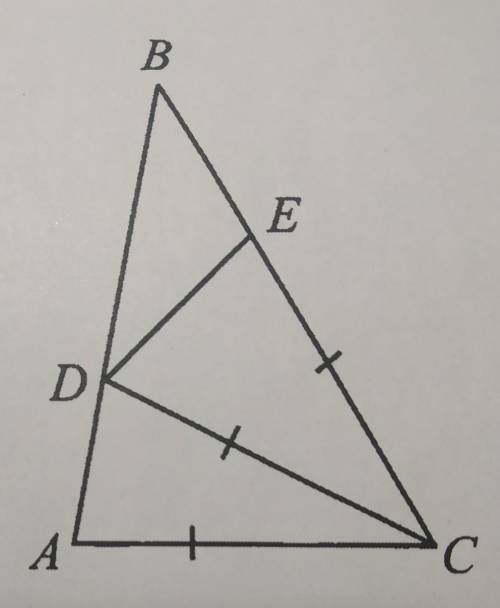
4. На рисунке ^ACD и ^DEC равнобедренные, <BDE = 30°. Могут ли быть равны ^DЕС и ^ADC, если <A = 80°? Найдите <BED , дано найти решение

Для решения данной задачи, обратимся к данным и известным свойствам треугольников.

Первое, что нам сообщается, это то, что треугольники ^ACD и ^DEC являются равнобедренными. Это означает, что стороны AC и AD равны между собой, а стороны DE и DC также равны.

Затем у нас есть угол BDE, который равен 30°. Мы знаем, что сумма углов в треугольнике равна 180°, поэтому угол BDE + угол BED + угол EDB должны равняться 180°. Из этого следует, что угол BED + угол EDB = 150°.

Теперь, давайте рассмотрим вопрос, могут ли быть углы ^DEC и ^ADC равными, если угол A равен 80°. Для этого нам нужно использовать свойство равнобедренных треугольников, которое гласит, что базы равнобедренных треугольников равны. В данном случае, базы треугольников ^ACD и ^DEC это отрезки AC и DE. Исходя из условия, сторона AC равна стороне AD, а сторона DE равна стороне DC.

Если бы углы ^DEC и ^ADC были равными, то треугольник ^DEC был бы равнобедренным и сторона DE была бы равна стороне DC. Но на рисунке видно, что сторона DE не равна стороне DC, поэтому углы ^DEC и ^ADC не могут быть равными.

И наконец, чтобы найти угол BED, нам нужно вычислить разницу между суммой углов BDE и BED (которая равна 150°) и углом BDE (который равен 30°). То есть, угол BED = 150° - 30° = 120°.

Таким образом, ответ на вопрос задачи: углы ^DЕС и ^ADC не могут быть равными, и угол BED равен 120°.