4. Известно, что а^с=b^c=30° 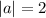
Вычислите:
(a+b)c
p.s. это все вектора
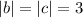
Другие вопросы по теме Математика
Популярные вопросы
- Какие заболевания человека вызываются бактериями? выберите 3 верных утвержд....
1 - Произведите синтаксический разбор предложения: в вагоне я не люблю разговаривать...
2 - Два щенка щека к щеке щиплют щётку в уголке.у четырёх черепашек по четыре...
3 - Какие регионы россии и откуда переселяются беженцы и вынужденные переселенцы...
3 - Скільки коренів має рівняння? ; sin x = sin 1...
2 - Как перевести на : в ноябре у моего брата день рождение...
3 - Какие события можно назвать началом смуты?...
3 - Найдите периметр прямоугольного участка земли площадь которого равна 18000...
3 - Катеты прямоугольного треугольника равны 7 см и 24 см. вычисли: - радиус...
3 - 1. как вы понимаете смысл названия рассказа судьба человека ? 2. почему...
2
У нас даны следующие условия:
а^с = b^c = 30°
|a| = 2
|b| = |c| = 3
Для начала разберемся с тем, что означают эти условия.
а^с и b^c - это обозначение углов между векторами а и с, и между векторами b и c соответственно. Значение этих углов равно 30°.
|a|, |b|, |c| - это обозначение длин векторов а, b и с. Длина вектора а равна 2, а длины векторов b и c равны 3.
Теперь перейдем к решению задачи. Нам нужно вычислить выражение (a+b)c.
1. Начнем с вычисления суммы векторов а и b. Сумма векторов это просто сложение их координат. Учитывая, что координаты вектора а имеют модуль 2, а координаты векторов b и c имеют модуль 3, получаем:
а + b = (2, 0) + (3, 0) = (2+3, 0) = (5, 0)
2. Теперь у нас есть новый вектор (5, 0). Умножим его на вектор с. Учитывая, что угол между этими векторами равен 30°, используем формулу для произведения векторов:
(5, 0)*c = |(5, 0)|*|c|*cos(30°)
3. Теперь посчитаем значение выражения |(5, 0)|*|c|*cos(30°). У нас значение модуля вектора (5, 0) равно 5, значение модуля вектора c равно 3. Тогда:
|(5, 0)|*|c|*cos(30°) = 5*3*cos(30°)
4. Найдем значение cos(30°). Воспользуемся таблицей значений тригонометрической функции:
cos(30°) = √3/2
5. Подставляем значение cos(30°) в формулу и считаем:
5*3*√3/2 = (15√3)/2
Таким образом, искомое выражение (a+b)c равно (15√3)/2.
Надеюсь, что объяснение было понятным и полезным для вас. Если у вас возникли еще вопросы, не стесняйтесь задавать!