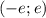4)Исследовать сходимость числового ряда
5)Найти интервал сходимости степенного ряда
Другие вопросы по теме Математика
Популярные вопросы
- Почему океаническая плита погружается под материковую?...
1 - Мне нужен ответ на по чтению, 2 класса. стр 22-23...
2 - Запишите число в виде суммы разрядных слагаемых число а)49532 б)1102350...
2 - :1. наименьшее положительное целое число 2. наибольшее отрицательное целое...
2 - 2-х художников и их произведения, в которых отразились верования славян....
2 - Найдите наибольший общий делитель чисел 12 и 18 50 и 175 675 и 825 7920 и...
1 - Из двух городов расстояние между которыми 90 км одновременно в одном направлении...
1 - Продолжите предложение авторская идея в рассказе темные аллеи заключается...
1 - Виділіть рядок, у якому всі слова мають однакову кількість звуків і букв:...
3 - Краткая запись к 3 класса про трактора было 20 тракторов на одно поле отправили...
1
____________________________________________________________
А значит ряд сходится при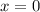
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
Условие можно интерпретировать иначе:
ответ: