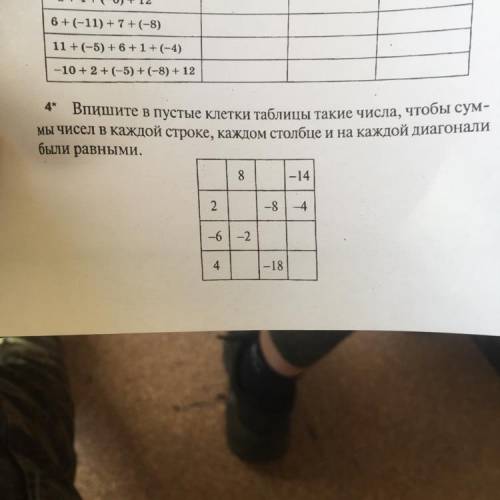
4* Bпишите в пустые клетки таблицы такие числа, чтобы сум- Мы чисел в каждой строке, каждом столбце и на каждой диагонали
были равными.
8 1-14
2
-8-4
-61-2
4
1-18

Добрый день! Я буду выступать в роли вашего школьного учителя и помогу вам решить данную задачу.

Чтобы найти числа, которые нужно вписать в пустые клетки таблицы таким образом, чтобы суммы чисел в каждой строке, каждом столбце и на каждой диагонали были равными, мы должны использовать метод системы уравнений.

Для начала, давайте посмотрим на саму таблицу. У нас есть некоторые известные числа, которые выделены жирным шрифтом.

8 1 -14
2 __ -4
-8 __ -2
_ __ -18

Для нахождения оставшихся чисел, давайте предположим, что в пустые клетки мы вписываем переменные. Выглядеть это будет следующим образом:

8 1 -14
2 a -4
-8 b -2
c d -18

Теперь, чтобы суммы чисел в каждой строке были равными, мы можем составить систему уравнений, где сумма чисел в первой строке равна сумме чисел во второй, третьей и четвертой строках.

8 + 1 - 14 = 2 + a - 4 + (-8) + b - 2 + c + d - 18

Мы можем упростить это уравнение:

-5 = a - 10 + b + c + d

Теперь посмотрим на столбцы. Сумма чисел в первом столбце равна сумме чисел во втором и третьем столбцах.

8 + 2 - 8 + c = 1 + a + b + d

Мы также можем упростить это уравнение:

2 + c = a + b + d - 7

Также у нас есть диагонали. Сумма чисел на первой диагонали равна сумме чисел на второй диагонали.

8 - 4 - 18 = -14 + a - 8 + 1 + b - 2

Мы можем это упростить:

-14 = -21 + a + b

Теперь у нас есть система трех уравнений:

-5 = a - 10 + b + c + d
2 + c = a + b + d - 7
-14 = -21 + a + b

Давайте решим эту систему.

Сначала возьмем третье уравнение и избавимся от отрицательного знака:

-14 - (-21) = a + b

-14 + 21 = a + b

7 = a + b

Теперь возьмем первое уравнение и выразим d:

d = -a - b - c + 15

Теперь возьмем второе уравнение и подставим наше выражение для d:

2 + c = a + b + (-a - b - c + 15) - 7

Упростим это выражение:

2 + c = 15 - 7 - c

Приравняем c:

2c = 8

c = 4

Теперь вернемся к первому уравнению и подставим наши значения a и b:

-5 = (-a - b - 4) + 15

Упростим это выражение:

-5 = 11 - a - b

-16 = -a - b

16 = a + b

Из системы у нас получились следующие значения переменных:

a + b = 16
c = 4
d = -a - b - c + 15

Осталось только найти значения a и b, используя эти уравнения. Обычно в школьной задаче мы должны найти только одно решение, но в данном случае есть много комбинаций значений a и b, которые будут удовлетворять нашим требованиям.

Например, возьмем a = 8 и b = 8. Подставим их в уравнения:

a + b = 16
8 + 8 = 16

c = 4

d = -a - b - c + 15
- 8 - 8 - 4 + 15 = -5

Таким образом, одно из возможных решений может быть:

8 1 -14
2 8 -4
-8 8 -2
4 -5 -18

Однако, помимо этого решения, есть и другие возможные комбинации значений a и b, которые также будут удовлетворять условиям задачи.

Итак, мы нашли одно из возможных решений задачи. Учтите, что это не единственное решение, и существует множество комбинаций значений a и b, которые будут удовлетворять условиям задачи.

Надеюсь, я смог помочь вам понять данную задачу. Если у вас есть еще вопросы, не стесняйтесь задавать их.