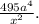№356 Ю.М. Колягин, 10 класс. Максимально подробно . Найти пятый член разложения бинома
( а/√x+√x/а)^m , если коэффициент третьего члена равен 66
Другие вопросы по теме Математика
Популярные вопросы
- План самостоятельной работы учащегося 5 класса по русскому языку. Четверть...
2 - ПЕРЕПЕСТИ НА РУССКИЙ ЯЗЫК ФОТО 2 часть...
3 - Ароматические углеводороды...
2 - 1)(m+2)(m+2) 2) (2a+b)(2a+b)...
3 - Назвіть найбільші озера України які вони за пожодженням...
3 - 9 Длина отрезка Ас больше длины отрезка CD на 4 см, а длина отрезка CD...
1 - Решить СИСТЕМОЙ УРАВНЕНИЯ с« { »такими скобками 5. Эльмира купила 3,5кг...
1 - Во сколько раз уменьшится сила тяжести ,eсли тело удалить от поверхности...
3 - Ребята что мне делать тест проходил и нечайно нажал не тот ответ и у...
3 - Сколько рублей дал Платов за работу левше?! ОЧЕНЬ...
3
Пошаговое объяснение:
Коэффициент третьего члена разложения бинома Ньютона равен:
Коэффициент пятого члена разложения бинома Ньютона равен:
Пятый член разложения бинома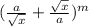 равен:
равен:
ответ: