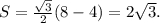3. Сумма двух сторон треугольника равна 4, а угол между ними 120°. Найдите наиболь- шую возможную площадь треугольника.
Другие вопросы по теме Математика
Популярные вопросы
- Равносторонний конус имеет высоту a. Найти площадь полной поверхности правильной...
3 - Write much or many. How boys are there in your class? How meat do you eat...
3 - Для приготовления сплава берётся 17 частей золота,2,5 части меди и 1,5 части...
2 - НАДЕЖДА ТОЛЬКО НА ВАС! знайдіть периметр многокутника, який утворився внаслідок...
2 - Паровой молот мощностью 390 кВт получает от нагревателя за 1,4 час количество...
3 - Сколько надо взять хлорида калия для приготовления 3кг 55 раствора...
2 - Найди неизвестные значения величин по формуле работы A=w*t A w t 60шт 4шт./ч...
1 - Установите соответствие: 1) Михаил Романов а) русско-турецкая война 2) Алексей...
2 - Берилген сан есимдерды катыстырып сойлем кура. Кураган сойлемдеринде олар...
1 - Чем изображается зависимость между величинами в прямоугольной системе координат?...
2
Пошаговое объяснение:
Пусть данные стороны имеют длины и
и 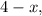 тогда по формуле площади
тогда по формуле площади 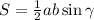 получаем
получаем 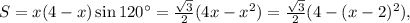 откуда понятно, что выражение в скобках будет наибольшим, когда будет наименьшим квадрат, то есть при
откуда понятно, что выражение в скобках будет наибольшим, когда будет наименьшим квадрат, то есть при 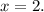
Тогда значение площади равно