3. Решите неравенство:
a) 3^х+2 -2*3^х < 12;
б) (log0,5 x)^2 + 3 log0,5 x – 4 < 0.
Другие вопросы по теме Математика
Популярные вопросы
- 34539кг выразить в тоннах, центнерах и килограмах...
3 - Ты любишь поспать в выходные? перевод...
2 - 1)каковы источники в хозяйстве? 2)что должен знать и уметь рачительный хозяин?...
1 - Шаровое скопление имеет 1 млн звезд главной последовательности, каждая из которых...
1 - Найти значения а, при которых уравнение ах^2+2х-3=0 имеет 2 совпавших корня...
1 - Напишите мини-сочинение, ответив на вопрос: положительный или отрицательный герой...
1 - Нужна ваша ! найдите корни квадратного уравнения : 3х2+6.1 х-5.4 0 решение обязательно...
2 - Передайте следующие предложения passive boice...
2 - Композиторы позднего барокко 1 антонио вивальди 2 клаудио монтевери 3 арканджело...
2 - Кто из иконописцев был родом из греции...
3
a)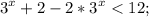
Число в любой степени всегда положительно, а значит оно при любом х будет больше отрицательного числа
ответ: x∈R
b)
Пусть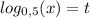 , тогда
, тогда
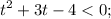
Разместим данные точки на координатной прямой
+ - +
₀₀>
-4 1 t
Исходя из рисунка, ответ t∈(-4;1)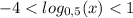 , то
, то
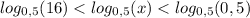
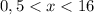
Вернёмся к замене
Если
Т.к. основание логарифма 0 < 0,5 < 1, то знаки поменяются на противоположные
ответ: x∈(0,5;16)