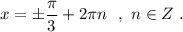2sin2x+10cosx-2sinx-5=0
может кто нибудь объяснить как это решается?
Другие вопросы по теме Математика
Популярные вопросы
- Масса двух чемоданов 20 кг,причём масса одного из них в три...
1 - Покажите на известных вам примерах влияние природных условий...
2 - Лодка за 2ч по течению реки путь,на 1.5 км меньший, чем путь...
3 - 2х(в квадрате)-5х-7=0 решить уравнение с дискриминантом : ((...
2 - Какой словообразования у слова отсутствие ? от какого слова...
3 - Сочинение на тему: правила или традиции любого народа не !...
3 - Как читается продал в предложении: мне подарили щенка,которого...
3 - Подчеркни буквы, которые не со звуками вороны-ворона вороны-ворон...
3 - Коса (инструмент) и коса (волосы); рысь (бег) и рысь (животное);...
3 - Даны 3 числа a b c возвести в квадрат только отрицательные черeз...
1
x=±π/3+2kπ, k∈Z
Пошаговое объяснение:
sin2a=2sinacosa
2sin2x+10cosx-2sinx-5=0
4sinxcosx+10cosx-2sinx-5=0
4sinxcosx-2sinx+10cosx-5=0
2sinx(2cosx-1)+5(2cosx-1)=0
(2sinx+5)(2cosx-1)=0
1) 2sinx+5=0
2sinx=-5
sinx=-2,5<-1⇒x∈∅
2) 2cosx-1=0
cosx=0,5
x=±arccos0,5+2kπ=±π/3+2kπ, k∈Z
Воспользуемся формулой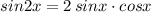 .
.
Произведение равно нулю, когда хотя бы один из множителей равен 0 .
Так как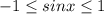 , то sinx не может быть равен -2,5 и
, то sinx не может быть равен -2,5 и
уравнение не имеет решений .
ответ: