285. Вычислите значение выражения -2

✓50-✓32/✓8
А) 3
B) 1/4
C) 4
D) 3✓2
E) 1/2

Верхняя -2 это степень

Ответы

Arsen2045 28.06.2021 16:00

C) 4.

Пошаговое объяснение:

(✓50-✓32)/✓8 = (5✓2 - 4✓2)/✓(2√2) = √2/(2√2) = 1/2.

Если всё это выражение первоначально возводилось в степень -2, то решение следующее:

(1/2) ^(-2) = 2^2 = 4.

ПОКАЗАТЬ ОТВЕТЫ

fgttyf 28.06.2021 16:00

C) 4.

Пошаговое объяснение:

Нам дано выражение: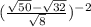 $(\frac{\sqrt{50}-\sqrt{32} }{\sqrt{8} })^{-2}$

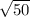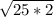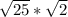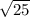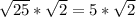Разберём каждый из корней подробно. $\sqrt{50}$ можно представить в виде: $\sqrt{25*2}$ . Мы знаем, что когда два числа перемножаются под одним корнем, то мы имеем право занести под отдельный корень каждое число: $\sqrt{25}*\sqrt{2}$ . Так как $\sqrt{25}$ , это 5, то получаем: $\sqrt{25}*\sqrt{2} =5*\sqrt{2}$ .

С первым корнем разобрались.

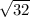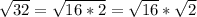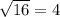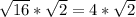Далее идёт $\sqrt{32}$ . Его также можно представить в виде произведения двух корней: $\sqrt{32}=\sqrt{16*2}=\sqrt{16} *\sqrt{2}$ . Так как $\sqrt{16} =4$ , получаем $\sqrt{16}*\sqrt{2} = 4*\sqrt{2}$ .

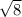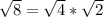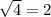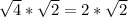Разберем знаменатель нашей дроби $\sqrt{8}$ . Данный корень можно как и два предыдущих, представить в виде произведения двух корней: $\sqrt{8} =\sqrt{4} *\sqrt{2}$ . Так как $\sqrt{4} =2$ , запишем: $\sqrt{4}*\sqrt{2} =2*\sqrt{2}$ .

Преобразуем наше выражение, с получившимися значениями:

$(\frac{5*\sqrt{2}-4*\sqrt{2}}{2*\sqrt{2}})^{-2}$

Преобразуем числитель, производя вычитание:

$(\frac{5*\sqrt{2}-4*\sqrt{2}}{2*\sqrt{2}})^{-2}=(\frac{\sqrt{2}}{2*\sqrt{2}})^{-2}$

Далее, мы имеем право сократить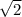 $\sqrt{2}$ в числителе и знаменателе:

$(\frac{\sqrt{2}}{2*\sqrt{2}})^{-2}=(\frac{1}{2})^{-2}$

Теперь стоит вспомнить свойство отрицательных степеней: число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем будет данное число с положительным показателем, то есть:

$a^{-b}=\frac{1}{(a)^b}$

То есть наша дробь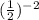 $(\frac{1}{2})^{-2}$ будет иметь вид:

$(\frac{1}{2})^{-2}=\frac{1}{(\frac{1}{2})^2}=\frac{1}{(\frac{1}{2}*\frac{1}{2})}=\frac{1}{\frac{1}{4}}$

Теперь чтобы вернуть дробь в нормальное состояние мы поделим одну дробь на другую, представив единицу в числителе в виде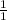 $\frac{1}{1}$ и записав их как произведение двух дробей, при этом перевернув во второй дроби числитель со знаменателем местами: