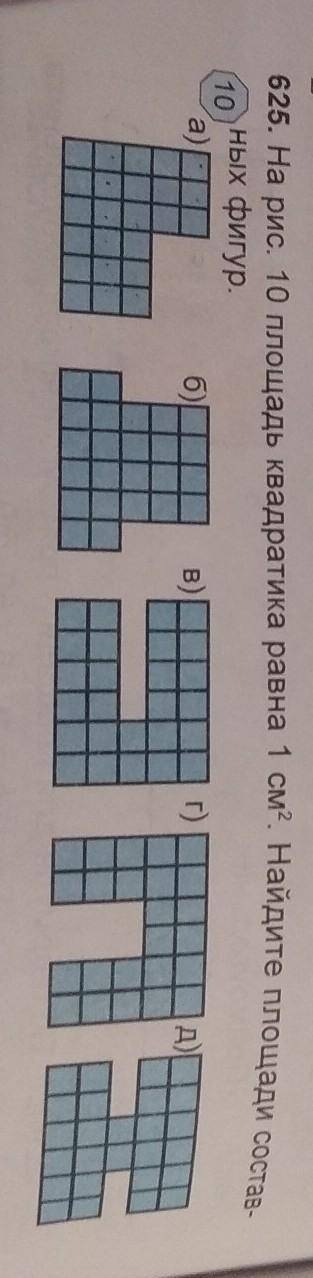
25. На рис. 10 площадь квадратика равна 1 см^2. Найдите площади составных фигур.​

Для решения этой задачи, нам нужно найти площади составных фигур, составленных из данных квадратиков. Мы можем использовать прямоугольник, образованный из двух квадратиков, и прямоугольный треугольник, образованный из одного квадратика.

1. Начнем с прямоугольника. У нас есть два квадратика, один над другим. Квадратики имеют одинаковую площадь в 1 см^2 каждый. Площадь прямоугольника равна произведению длины на ширину, поэтому площадь прямоугольника будет равна 1 см^2 * 2 = 2 см^2.

2. Затем рассмотрим прямоугольный треугольник. Мы можем использовать один квадратик, чтобы образовать прямоугольный треугольник. Площадь треугольника равна половине произведения длины основания и высоты. В данной ситуации, длина основания равна длине одной стороны квадратика, которая равна 1 см, а высота равна длина другой стороны квадратика, которая также равна 1 см. Поэтому площадь прямоугольного треугольника будет равна 1 см * 1 см / 2 = 0.5 см^2.

Таким образом, площадь составной фигуры в задаче равна 2 см^2 + 0.5 см^2 = 2.5 см^2.