24.1. Упростите выражение: 1) sin(60° + а) + sin(a — 60);
3) sin(30° + а) – sin(30°- а);
2) cos(60° + а) + cos(а — 60°);
4) cos(30° + а) - cos(30°- а);
те
нужно
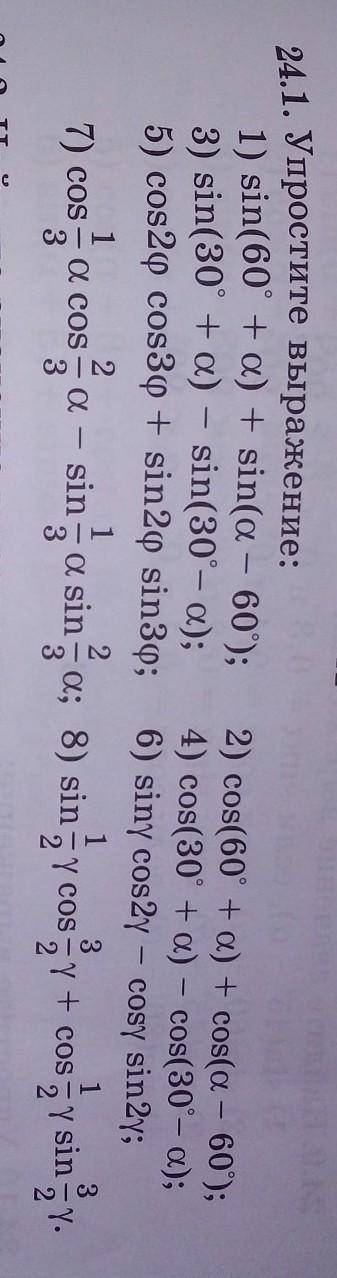
Другие вопросы по теме Математика
Популярные вопросы
- Алгебра Докажите, что значение выражения кратно...
1 - Расстояние между параллельными прямыми тип равно 10 см, а расстояние...
3 - тест по химии 8 кл тест по химии 8 кл >...
1 - Приведите подобные слогаемые 2х+5у-1,7х-5,8у= 3 а...
3 - Какой ответ, скажите Какой ответ, скажите...
1 - Подставите буквы НУЖНО ОЧЕНЬ Подставите буквы НУЖНО ОЧЕНЬ...
1 - . Используя данные рисунка, найдите длину ОС, если 0В = 6 см....
2 - Знайдить два нерозгоонути кути, утворени при перетини двох прямих...
3 - ХЕЛП Найди коэффициент произведения: −6⋅a⋅(−4)...
2 - Рассказ МАЛЕНЬКИЙ ПРИНЦ А.11. Прибыв на Землю, какое разочарование...
3
1) Начнем с первого выражения: sin(60° + а) + sin(a — 60).
Для упрощения данного выражения воспользуемся тригонометрической формулой синуса суммы двух углов: sin(x + y) = sin(x) * cos(y) + cos(x) * sin(y).
Подставим данную формулу в первое выражение:
sin(60° + а) + sin(a — 60) = sin(60°) * cos(а) + cos(60°) * sin(а) + sin(a) * cos(60°) - cos(a) * sin(60°).
Заметим, что sin(60°) = √3/2 и cos(60°) = 1/2. Подставим эти значения:
(√3/2) * cos(а) + (1/2) * sin(а) + sin(a) * (1/2) - cos(a) * (√3/2).
Далее группируем слагаемые с синусами и слагаемые с косинусами:
[(√3/2) * cos(а) + sin(a) * (1/2)] + [(1/2) * sin(а) - (√3/2) * cos(a)].
Теперь проведем раскрытие скобок:
(√3/2) * cos(а) * sin(a)/2 + sin(a)/2 - (√3/2) * cos(a) * sin(a)/2 - (√3/2) * cos(a).
Заметим, что у слагаемых с тригонометрическими функциями sin и cos в числителях стоит 1/2, что позволяет их объединить и упростить:
1/2 * sin(a) - (√3/2) * cos(a).
Это будет окончательным упрощенным видом данного выражения.
2) Переходим ко второму выражению: sin(30° + а) – sin(30° - а).
Для упрощения воспользуемся тригонометрической формулой синуса разности двух углов: sin(x - y) = sin(x) * cos(y) - cos(x) * sin(y).
Подставим данную формулу во второе выражение:
sin(30° + а) - sin(30° - а) = sin(30°) * cos(а) - cos(30°) * sin(а) - sin(30°) * cos(а) + cos(30°) * sin(а).
Заметим, что sin(30°) = 1/2 и cos(30°) = √3/2. Подставим эти значения:
(1/2) * cos(а) - (√3/2) * sin(а) - sin(30°) * cos(а) + cos(30°) * sin(а).
Теперь группируем слагаемые с синусами и слагаемые с косинусами:
[(1/2) * cos(а) - sin(30°) * cos(а)] + [-(√3/2) * sin(а) + cos(30°) * sin(а)].
Проведем раскрытие скобок:
(1/2) * cos(а) * cos(30°) - sin(30°) * cos(а) - (√3/2) * sin(а) * sin(30°) + cos(30°) * sin(а).
Заметим, что у слагаемых с тригонометрическими функциями sin и cos в числителях стоит 1/2 и √3/2 соответственно. Это позволяет их объединить и упростить:
(1/2) * cos(а) * cos(30°) - (√3/2) * sin(а) * sin(30°) - sin(30°) * cos(а) + cos(30°) * sin(а).
Таким образом, мы получили окончательный упрощенный вид второго выражения.
3) Переходим к третьему выражению: cos(60° + а) + cos(а - 60°).
Аналогично первому выражению, воспользуемся тригонометрической формулой косинуса суммы двух углов: cos(x + y) = cos(x) * cos(y) - sin(x) * sin(y).
Подставим данную формулу в третье выражение:
cos(60° + а) + cos(а - 60°) = cos(60°) * cos(а) - sin(60°) * sin(а) + cos(а) * cos(60°) - sin(а) * sin(60°).
Заметим, что cos(60°) = 1/2 и sin(60°) = √3/2. Подставим эти значения:
(1/2) * cos(а) - (√3/2) * sin(а) + cos(а) * (1/2) - sin(а) * (√3/2).
Группируем слагаемые с косинусами и слагаемые с синусами:
[(1/2) * cos(а) + cos(а) * (1/2)] + [-(√3/2) * sin(а) - sin(а) * (√3/2)].
Проведем раскрытие скобок:
(1/2) * cos(а) * cos(а) + cos(а) * (1/2) - (√3/2) * sin(а) * sin(а) - sin(а) * (√3/2).
У слагаемых с тригонометрическими функциями sin и cos в числителях стоит 1/2 и √3/2 соответственно. Это позволяет их объединить и упростить:
(1/2) * [cos(а) + cos(а)] - (√3/2) * [sin(а) + sin(а)].
Таким образом, мы получили окончательный упрощенный вид третьего выражения.
4) Переходим к четвертому выражению: cos(30° + а) - cos(30° - а).
Аналогично второму выражению, воспользуемся тригонометрической формулой косинуса разности двух углов: cos(x - y) = cos(x) * cos(y) + sin(x) * sin(y).
Подставим данную формулу в четвертое выражение:
cos(30° + а) - cos(30° - а) = cos(30°) * cos(а) + sin(30°) * sin(а) - cos(30°) * cos(а) + sin(30°) * sin(а).
Заметим, что cos(30°) = √3/2 и sin(30°) = 1/2. Подставим эти значения:
(√3/2) * cos(а) + (1/2) * sin(а) - (√3/2) * cos(а) + (1/2) * sin(а).
Группируем слагаемые с косинусами и слагаемые с синусами:
[(√3/2) * cos(а) - (√3/2) * cos(а)] + [(1/2) * sin(а) + (1/2) * sin(а)].
Таким образом, мы получили окончательный упрощенный вид четвертого выражения.
Все упрощения были выполнены с использованием тригонометрических формул синуса и косинуса суммы или разности двух углов. Если у вас возникли дополнительные вопросы по решению, не стесняйтесь задавать их. Я готов помочь вам разобраться в задаче!