237.
(2; 10) и (-3; 1) - это конечные точки диаметра круга. Нарисуйте этот круг.

Ответы

Sabico 18.08.2020 15:18

Определим координаты диаметра: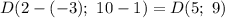 $D(2 - (-3); \ 10 - 1) = D(5; \ 9)$

Определим длину диаметра: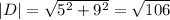 $|D| = \sqrt{5^{2} + 9^{2}}= \sqrt{106}$

Тогда радиус окружности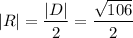 $|R| = \dfrac{|D|}{2} = \dfrac{\sqrt{106}}{2}$

Определим координаты центра, используя уравнение окружности:

$(x - x_{0})^{2} + (y - y_{0})^{2} = R^{2}$

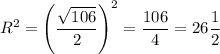Здесь $R^{2} = \left(\dfrac{\sqrt{106}}{2} \right)^{2} = \dfrac{106}{4} = 26\dfrac{1}{2}$ , а и 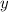— координаты точек, лежащих на окружности.

$\displaystyle \left \{ {{(2 - x_{0})^{2} + (10 - y_{0})^{2}} = 26\dfrac{1}{2} \atop {(-3 - x_{0})^{2} + (1 - y_{0})^{2}} = 26\dfrac{1}{2}}} \right.$

$\displaystyle \left \{ {{x_{0}^{2} - 4x_{0} + y_{0}^{2} - 20y_{0} = - 77\dfrac{1}{2} \atop {x^{2}_{0} + 6x_{0} + y^{2}_{0} - 2y_{0} = 16\dfrac{1}{2} \ \ \ \ \right.$

Вычтем из второго уравнения первое:

$10x_{0} + 18y_{0} = 94$

$5x_{0} + 9y_{0} = 47$

$x_{0} = \dfrac{47 - 9y_{0}}{5} = \dfrac{47}{5} - \dfrac{9y_{0}}{5}$

Подставим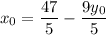 $x_{0} = \dfrac{47}{5} - \dfrac{9y_{0}}{5}$ во второе уравнение:

$\left(\dfrac{47}{5} - \dfrac{9y_{0}}{5} \right )^{2} + 6\left(\dfrac{47}{5} - \dfrac{9y_{0}}{5} \right) + y^{2}_{0} - 2y_{0} = 16\dfrac{1}{2}$

$\dfrac{(47 - 9y_{0})^{2}}{25} + \dfrac{6(47 - 9y_{0})}{5} + y_{0}^{2} - 2y_{0} = \dfrac{33}{2}$

$\dfrac{2209 - 846y_{0} + 81y_{0}^{2}}{25} + \dfrac{282 - 54y_{0}}{5} + y^{2}_{0} - 2y_{0} = \dfrac{33}{2}$

$2(2209 - 846y_{0} + 81y_{0}^{2}) + 10(282 - 54y_{0}) + 50y^{2}_{0} - 100y_{0} = 825$

$6413 - 2332y_{0} + 212y_{0}^{2} = 0$

$4y_{0}^{2} - 44y_{0} + 121 = 0$

$(2y_{0} - 11)^{2} = 0$

$2y_{0} - 11 = 0$

$y_{0} = \dfrac{11}{2}$

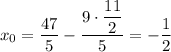
Тогда $x_{0} = \dfrac{47}{5} - \dfrac{9 \cdot \dfrac{11}{2} }{5} = -\dfrac{1}{2}$

Следовательно, уравнение окружности:

$\left(x + \dfrac{1}{2} \right)^{2} + \left(y - \dfrac{11}{2} \right)^{2} = 26\dfrac{1}{2}$

Окружность изображена на плоскости (см. вложение).

237.(2; 10) и (-3; 1) - это конечные точки диаметра круга. Нарисуйте этот круг.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

незнайка1187 18.02.2021 16:24

Розв,яжить ривняння (x - 3,5 ) - 1,2= - 0,2...

missmekhtiyeva110803 18.02.2021 16:24

Начертить прямоугольный параллепипед. Обозначить его. Записать пары параллельных плоскостей. ответ доказать...

Лолери 18.02.2021 16:25

В ПИЦЦЕРИЮ ПОСТУПАЮТ ЗАКАЗЫ НЕ ТОЛЬКО НА ПИЦЦЫ НО И НА КУСКИ. ПОВАР САМ ПРИНИМАЕТ ВИДИТ НА ТАБЛО КОЛИЧЕСТВО КУСКОВ КОТОРЫЕ ЗАКАЗАЛИ ПОСЕТИТЕЛИ. ПОВАР САМ ПРИНИМАЕТ РЕШЕНИЕ...

nikolaenko0473 18.02.2021 16:27

−15,64−(−34,24)−24,68−(−4,48)+(−81,2)...

den6580 18.02.2021 16:27

Выполни : 1) 2,3 ∙ 0,4 2) 0,07 ∙ 6,9 3) 1,13 ∙ 4,5 4) 0,25 ∙ 0,48 5) 4,7 ∙ 6,31 6) 0,007 ∙ 0,2 7) 0,05 ∙ 2,3 8) 7,41 ∙ 1,9 9)...

youngfng 18.02.2021 16:27

414. Перепишите дроби в десятичной форме. a)15/100b)1 2/10с)107/1000...

zlooo2 18.02.2021 16:27

10Сколько квадратов изобратено на рисункаПридумай свои похожие планияП6)...

Гоша2285 18.02.2021 16:28

Света купила 8 карандашей по цене x руб. за карандаш, а Таня купила 2 ручки по цене в 1,7 раза выше, чем цена за карандаш. После этого у девочек осталось 48,3 руб. Какая...

нигяр121 18.02.2021 16:28

4x-3y+y (2y-3x)=0 кто знает напишите решение, предмет Дифф.уравнение...

UlyanaAleks 18.02.2021 16:29

382. Скорость автомобиля 84 км/час. Сколько метров он проедет за7 минут...

237.(2; 10) и (-3; 1) - это конечные точки диаметра круга. Нарисуйте этот круг.​

Популярные вопросы

237.
(2; 10) и (-3; 1) - это конечные точки диаметра круга. Нарисуйте этот круг.