23. Биссектрисы углов при стороне CD параллелограмма ABCD пересе- каются в точке Р. Найдите CD, если CP = 7, DP = 24.
Другие вопросы по теме Математика
Популярные вопросы
- X+2-6(x-6)=6(6-x)+6 (решите уравнение)...
2 - Явас составьте текст с пятью предложениями, озаглавьте, в каждом предложении должны...
3 - Гравировщик делает таблички с буквами. одни и те же буквы он гравирует за одинаковое...
2 - Звуковая модель слова дятел яйцо ( - твердая согласная 0 гласная = мягкая согласная)...
3 - Составить утвердительные предложения из этих вопросов is it cold in your room?...
1 - Какой самый большой остров и полуостров ?...
1 - Укажите риторическую фигуру, использованную в высказывании: книжный голод не проходит:...
1 - На какую тему можно сделать стенгазету по ?...
1 - Моторная лодка движется вниз по течению реки со скоростью 15 км/ч относительно...
1 - Как изменится период свободных колебаний маятника, если его перенести с полюса...
2
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
△CND — равнобедренный с основанием ND.
Так как биссектриса ∠DCN проведена к основанию равнобедренного треугольника, то она является еще и высотой.
Значит, CP ⊥ ND и ∠CPD = 90°.
Рассмотрим прямоугольный △ CPD.
По теореме Пифагора, CD² = CP² + DP².
Отсюда,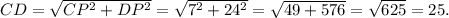
ответ: CD = 25.