2 задачи на теорию вероятности. 1.В группе имеется 19 студентов, среди которых 3 – отличника. По списку наудачу отобрано 5 студентов.
Найти вероятность того, что среди отобранных студентов не более 3 отличников.
2.В ящике находятся 13 деталей, из которых окрашено 4. Сборщик наудачу взял три детали. Найти вероятность того, что будут окрашены не более двух деталей.
Заранее очень благодарен.
Другие вопросы по теме Математика
Популярные вопросы
- Наведіть формули відомих вам вуглеводнів, які не мають ізомерів...
1 - Copy and complete the table with these time expressions. yesterday, tomorrow,...
1 - Как будет писаться на слова « приходить , звонить , играть, нравится» в past...
1 - Укажите 2 политических 2 и 2 социальных последствий -джунгарского нашествия...
2 - Log5((x^2)-6x+13)=2log4(x-1)*log(x-1)(2)...
2 - 1)дано: w(h)=14,33% д(h₂)=28,06 знайти: cₓhy 2)дано: w(c)=75% д(повітря)=0,552...
3 - [tex]3^{\sqrt{2x-1} } *27=9^{\sqrt{2x-1} }[/tex] [tex]9^{x}: \sqrt{3^{x} }=3\sqrt[3]{9}:...
1 - Если сторону квадрата увеличить на 20% то его площадь увеличится на 176м2. вычисли...
1 - Вет: 0выполните эскиз детали по её описанию, нанесите размеры: титановысток...
3 - Кчастному чисел 640 и 8 прибавь а,если а = 0, 10, 100. из а вычти частное чисел...
2
1) 1; 2) 141/143
Пошаговое объяснение:
1) Вероятность того, что среди отобранных студентов будет больше 3 отличников равна нулю, так как в классе всего 3 отличника. Тогда вероятность не более трёх отличников равна 1.
2) Необходимо найти вероятность того, что среди взятых наудачу 3 деталей либо 2, либо 1, либо 0 будут окрашенными.
Посчитаем число комбинаций с подобным исходом.
Комбинации, при которых взято 2 из 4 окрашенных и 1 из 9 неокрашенных деталей: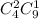
Комбинации, при которых взято 1 из 4 окрашенных и 2 из 9 неокрашенных детали: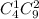
Комбинации, при которых взято 0 из 4 окрашенных и 3 из 9 неокрашенных детали: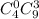
Получаем, что суммарное число комбинаций, удовлетворяющих нашему условию: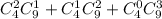
Теперь посчитаем число комбинаций при взятии 3 случайных деталей, вне зависимости от их окраски: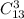
Тогда вероятность получить не более 2 окрашенных деталей: