2. Точка M – середина отрезка AB. Найдите координаты точки B, если A (1;3;-2), M (-2;4;5). а) B (-5;5;12);
в) B (-1;5;7);
б) B (3;5;8);
г) другой ответ.
3. Катеты прямоугольного треугольника равны 5 см и 6 см . Найдите площадь проекции этого треугольника на плоскость, если плоскость треугольника наклонена к плоскости проекции под углом 600.
а) 7,5 см2; в) 30 см2;
б) 15 см2;
г) другой ответ.
4. Из точки, отстоящей от плоскости на расстоянии 4, проведены две наклонные к плоскости под углом 450. Найдите длины наклонных.
а) 4 и 4;
в) 3 и 3;
б) 2 и 2;
г) другой ответ.
5. Угол между единичными векторами и равен 600. Найдите абсолютную величину вектора +.
а) 1;
в) ;
б) ;
г) другой ответ.
6. Найдите длину AM – медианы треугольника ABC, если A (1;2;3), B (6;3;6), C (-2;5;2).
а) ;
в) 3;
б) 2;
г) другой ответ.
7. Какой из данных углов наибольший, если A (1;1;1), B (4;2;2), C (3;0;1), D (3;-1;2).
а) АBС
в) DCA
б) BCD
г) DAB
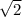

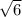
Другие вопросы по теме Математика
Популярные вопросы
- Реши задачу, пошагово выполняя указанные действия и заполняя пропуски. Ракета...
2 - ответить на вопрос!Почему воздух можно легко сжать?...
2 - Сделать мини собщенее буквально на 1.30мин про Бетховена по критериям: 1. Привести...
1 - Заполнить иск В Арбитражный суд Истец: (наименование, место нахождения, если...
3 - 1 вариант алгебра 7 клас ...
3 - Ребят нужна кто 1до4 класса тому я ...
2 - во сколько раз увеличивается скорость реакции, если температурный коэффициент...
3 - Аққулар ұйықтағанда поэмасының құдіреті эссе...
2 - примеры на картинке поскорей.Даю 20б...
2 - 6. Інтелектуальне самопочуття - це: а) здатність людини пізнавати й використовувати...
2
а) B (-5;5;12):
X-координата B: (1 + (-5)) / 2 = -4 / 2 = -2
Y-координата B: (3 + 5) / 2 = 8 / 2 = 4
Z-координата B: (-2 + 12) / 2 = 10 / 2 = 5
Таким образом, координаты точки B для варианта а) равны (-2;4;5).
в) B (-1;5;7):
X-координата B: (1 + (-1)) / 2 = 0 / 2 = 0
Y-координата B: (3 + 5) / 2 = 8 / 2 = 4
Z-координата B: (-2 + 7) / 2 = 5 / 2 = 2.5
Таким образом, координаты точки B для варианта в) равны (0;4;2.5).
б) B (3;5;8):
X-координата B: (1 + 3) / 2 = 4 / 2 = 2
Y-координата B: (3 + 5) / 2 = 8 / 2 = 4
Z-координата B: (-2 + 8) / 2 = 6 / 2 = 3
Таким образом, координаты точки B для варианта б) равны (2;4;3).
г) другой ответ:
Для этого варианта нам необходимо использовать тот же подход, используя свойство середины отрезка и координаты точки M. Мы будем искать координаты точки B, а затем сравним их с данными в вариантах, чтобы понять, какой из них является правильным ответом.
3. Для нахождения площади проекции прямоугольного треугольника на плоскость нужно умножить длину одного катета на длину другого катета, а затем умножить результат на синус угла между плоскостью треугольника и плоскостью проекции.
Площадь = длина первого катета * длина второго катета * sin(угол между плоскостью треугольника и плоскостью проекции)
В данном случае, длины катетов равны 5 см и 6 см, а угол между плоскостью треугольника и плоскостью проекции равен 60 градусов.
а) 7,5 см2:
Площадь = 5 * 6 * sin(60) = 30 * √3 / 2 = 15√3 см2
Таким образом, площадь проекции равна 15√3 см2 для варианта а).
в) 30 см2:
Площадь = 5 * 6 * sin(60) = 30 * √3 / 2 = 15√3 см2
Таким образом, площадь проекции равна 15√3 см2 для варианта в).
б) 15 см2:
Площадь = 5 * 6 * sin(60) = 30 * √3 / 2 = 15√3 см2
Таким образом, площадь проекции равна 15√3 см2 для варианта б).
г) другой ответ:
Для этого варианта мы будем использовать тот же подход, но с заданными данными, чтобы найти площадь проекции. Затем сравним полученные результаты с данными в вариантах.
4. Чтобы найти длины наклонных, нам необходимо знать высоту, или расстояние, от точки до плоскости.
а) 4 и 4:
Если высота равна 4, то длины наклонных будут равны высоте. То есть, длины наклонных будут 4 и 4.
в) 3 и 3:
Если высота равна 3, то длины наклонных будут равны высоте. То есть, длины наклонных будут 3 и 3.
б) 2 и 2:
Если высота равна 2, то длины наклонных будут равны высоте. То есть, длины наклонных будут 2 и 2.
г) другой ответ:
Для каждого из вариантов мы должны использовать высоту, чтобы найти длины наклонных и сравнить их с данными в других вариантах.
5. Для нахождения абсолютной величины вектора в данном случае нам нужно найти модуль этого вектора.
а) 1:
Модуль вектора = √(1^2 + 1^2 + 1^2) = √3
Таким образом, абсолютная величина вектора равна √3 для варианта а).
в)
Модуль вектора = √(√2^2 + √2^2 + √2^2) = √6
Таким образом, абсолютная величина вектора равна √6 для варианта в).
б)
Модуль вектора = √(√3^2 + √3^2 + √3^2) = √9 = 3
Таким образом, абсолютная величина вектора равна 3 для варианта б).
г) другой ответ:
Для каждого из вариантов нам нужно найти модуль вектора и сравнить его с данными в других вариантах.
6. Для нахождения длины медианы треугольника мы можем использовать формулу для нахождения длины вектора.
Длина медианы = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
Где (x1; y1; z1), (x2; y2; z2) - координаты двух вершин, которые соединяет медиана, а А (1;2;3), В (6;3;6), С (-2;5;2).
Таким образом, для нахождения длины AM - медианы треугольника ABC, нужно использовать координаты точек A и M в формуле:
Длина AM = √((-2 - 1)^2 + (4 - 2)^2 + (5 - 3)^2) = √((-3)^2 + 2^2 + 2^2) = √(9 + 4 + 4) = √17
Таким образом, длина AM - медианы треугольника ABC равна √17.
7. Чтобы определить, какой из данных углов наибольший, нам необходимо найти косинусы углов и сравнить их значения.
а) АBС:
Вектор AB = (4 - 1; 2 - 1; 2 - 3) = (3; 1; -1)
Вектор AC = (3 - 1; 0 - 1; 1 - 3) = (2; -1; -2)
cos(АBC) = (3 * 2 + 1 * -1 + -1 * -2) / (√(3^2 + 1^2 + -1^2) * √(2^2 + -1^2 + -2^2)) = (6 - 1 + 2) / (√11 * √9) = 7 / (3√11) ≈ 0.68
в) DCA:
Вектор DC = (3 - 3; -1 - 0; 2 - 1) = (0; -1; 1)
Вектор DA = (3 - 1; -1 - 1; 2 - 1) = (2; -2; 1)
cos(DCA) = (0 * 2 + -1 * -2 + 1 * 1) / (√(0^2 + -1^2 + 1^2) * √(2^2 + -2^2 + 1^2)) = (0 + 2 + 1) / (√2 * √9) = 3 / (3√2) ≈ 0.53
б) BCD:
Вектор BC = (3 - 4; -1 - 2; 2 - 2) = (-1, -3, 0)
Вектор BD = (3 - 3; -1 - -1; 2 - 2) = (0, 0, 0)
Так как вектор BD равен нулевому вектору, то угол BCD не может быть определен.
г) DAB:
Вектор DA = (3 - 1; -1 - 2; 2 - 3) = (2; -3; -1)
Вектор DB = (3 - 3; -1 - -1; 2 - 3) = (0; 0; -1)
cos(DAB) = (2 * 0 + -3 * 0 + -1 * -1) / (√(2^2 + -3^2 + -1^2) * √(0^2 + 0^2 + -1^2)) = 1 / (3 * 1) = 1 / 3 ≈ 0.33
Итак, косинусы углов ABC, DCA и DAB равны примерно 0.68, 0.53 и 0.33 соответственно. Таким образом, угол ABC наибольший из предложенных вариантов. Ответ: а) ABС.