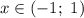№ 2. Решите неравенства 1)√(x+2)>x 2) √(х^2+3)<2
Другие вопросы по теме Математика
Популярные вопросы
- Между числами -10 и -810 вставьте три числа так, что бы всесте с данными...
3 - Важно! с рисунком 1) в наклонной четырехугольной призме основанием...
3 - Длина прямоугольника 20 сантиметров а ширина 12 сантиметров найдите...
3 - Папа серёжи и нади предлагает вам выберите правильные ответы и отметьте...
3 - Синтакс розбір речення терміново памятай, що любов - це насамперед...
3 - Каково сопротивление медного провода длинной 2м и площадью поперечного...
3 - Доброго времени суток! вот мой вопрос,если не сложно ответьте решением,а...
1 - Вчем особенность употребления существительных числительных местоимений...
3 - Из каких стран петр 1 : гаврилованный станок рубанок щипцы для вырывания...
3 - Отрезок bd - высота равнобедренного треугольника abc , угол abd =34°...
3
Неравенство вида равносильно:
равносильно:
Имеем:
Объединяем решения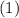 и
и 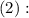
ответ: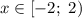
Неравенство вида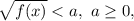 равносильно:
равносильно:
Имеем:
ответ: