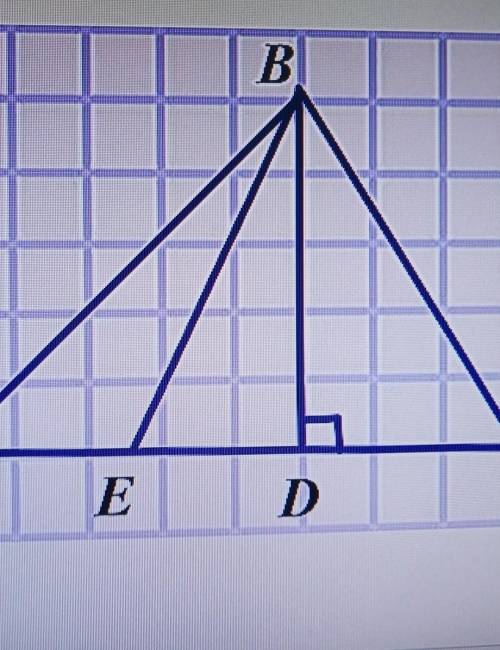
2. Реши задачу: Дано: AE=2, ED=2, DC=3, BD=3
Найдите площади всех треугольников,
изображенных на рисунке.​

Дана фигура, которая состоит из нескольких треугольников. Для решения задачи нам понадобится знание формулы для площади треугольника: S = 0.5 * a * h, где S - площадь треугольника, a - основание, h - высота.

Давайте рассмотрим каждый треугольник по отдельности и найдем их площади.

1) Треугольник AED:
У нас уже известны значения сторон AE и ED, поэтому нам необходимо найти высоту треугольника. По теореме Пифагора в прямоугольном треугольнике AED, где AE является гипотенузой, сумма квадратов катетов равна квадрату гипотенузы:

AE^2 = AD^2 + ED^2

Так как AD = DC + BD, подставим значения и решим уравнение:

4 = (DC + BD)^2 + 2^2
4 = (3 + 3)^2 + 4
4 = 36 + 4
4 = 40

У нас получилось неверное уравнение, поэтому мы делаем вывод, что заданные стороны AE, ED, DC и BD не могут образовать треугольник AED. Следовательно, площадь данного треугольника равна нулю.

2) Треугольник ABC:
Из рисунка видно, что треугольник ABC является прямоугольным, так как угол BAC прямой (это можно определить по перпендикулярным сторонам).
Следовательно, его площадь можно найти как половину произведения длин катетов:

S_ABC = 0.5 * AC * BC

AC = AE + ED + DC = 2 + 2 + 3 = 7
BC = BD + DC = 3 + 3 = 6

S_ABC = 0.5 * 7 * 6 = 21

Площадь треугольника ABC равна 21.

3) Треугольник ADB:
Для нахождения площади треугольника ADB нам понадобится длина основания и высота. Основание треугольника составляют стороны из точки A до точки D и из точки D до точки B.

AD = AE + ED = 2 + 2 = 4
DB = DC = 3

Теперь мы должны найти высоту треугольника ADB. Мы можем использовать пифагорову теорему, так как треугольник является прямоугольным:

DB^2 = AD^2 - AB^2

AB можно найти используя теорему Пифагора в треугольнике ABC:

AB^2 = AC^2 - BC^2
AB^2 = 7^2 - 6^2
AB^2 = 49 - 36
AB^2 = 13

Теперь найдем площадь треугольника ADB, используя формулу:

S_ADB = 0.5 * DB * h

DB = 3
h = AB = √13

S_ADB = 0.5 * 3 * √13 = 1.5√13

Площадь треугольника ADB равна 1.5√13.

Таким образом, площади треугольников AED и BDC равны нулю, а площади треугольников ABC и ADB равны 21 и 1.5√13 соответственно.