2. при якому значенні многочлен
х³ + 6х²+ах + 5 ділиться без остачі
на х²+ х+1

3. різниця квадратів двох послідовних натуральних чисел дорівнює 51. знайти більше число​

2) Представимо вираз у наступному вигляді

Перший доданок ділиться на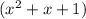 , а другий доданок буде ділитися на 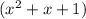при 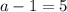звідси .

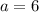Отже, при a = 6 многочлен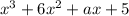 ділиться на 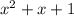без остачі.

Відповідь: 6.

3) Нехай два послідовні числа дорівнюють x і (x+1). Тоді складемо рівняння за умовою задачі.

Отже, шукані числа - 25 і 25 + 1 = 26.

Відповідь: 26.