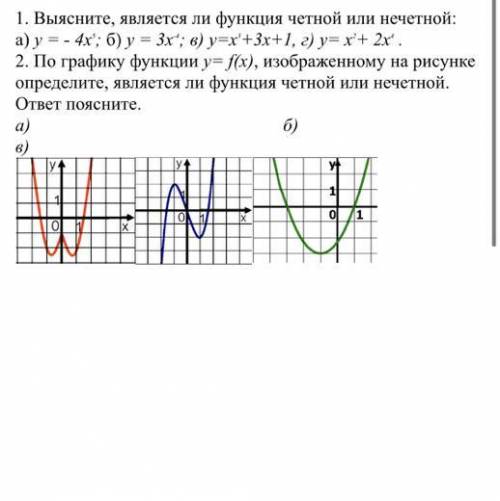
2. По графику функции у= f(x), изображенному на рисунке определите, является ли функция четной или нечетной. ответ поясните. а) б) в)

Для определения того, является ли функция четной или нечетной, мы можем использовать определение этих понятий.

Функция f(x) называется четной, если для любого значения x в области определения выполняется условие f(-x) = f(x). Другими словами, если мы возьмем любое значение x и заменим его на -x, то полученное значение функции должно совпадать с исходным значением.

Функция f(x) называется нечетной, если для любого значения x в области определения выполняется условие f(-x) = -f(x). В данном случае, если мы возьмем любое значение x и заменим его на -x, то полученное значение функции должно быть противоположным по знаку к исходному значению.

Обратите внимание на график функции у=f(x), изображенный на рисунке. Мы можем заметить, что график функции симметричен относительно оси y. Это означает, что если мы возьмем какую-либо точку на графике и отразим ее относительно оси y, то получим другую точку на том же графике. Это свойство аналогично свойству четных функций.

Теперь, чтобы определить, является ли функция четной или нечетной, нам нужно проверить выполнение условий для четности или нечетности.

а) Давайте возьмем какую-то точку на графике, например, (1, 3). Если функция является четной, то для x = -1 значение функции должно быть таким же, как для x = 1. Проверим: f(-1) = 3. Значение функции для x = -1 равно значению функции для x = 1.

Таким образом, мы можем заключить, что функция у=f(x) является четной.

б) Здесь на графике нет точки, которую мы могли бы использовать для проверки, поэтому мы не можем однозначно определить, является ли функция четной или нечетной только по этому фрагменту.

в) Если мы возьмем точку с координатами (-2, -1) и отразим ее относительно оси y, мы получим точку с координатами (2, 1). Проверим значение функции для этих точек: f(-2) = -1, -f(2) = -1. Они совпадают по значению, но противоположны по знаку.

Таким образом, мы можем заключить, что функция у=f(x) является нечетной.

Вывод: Функция у=f(x), изображенная на рисунке, является нечетной.