№2 Найти х, при которых f'(х)=0 f(x)=(5-2x (2x+1)
№3 Найти х, при которых f'(x)>0
3x-1
f(x) =
1-2х
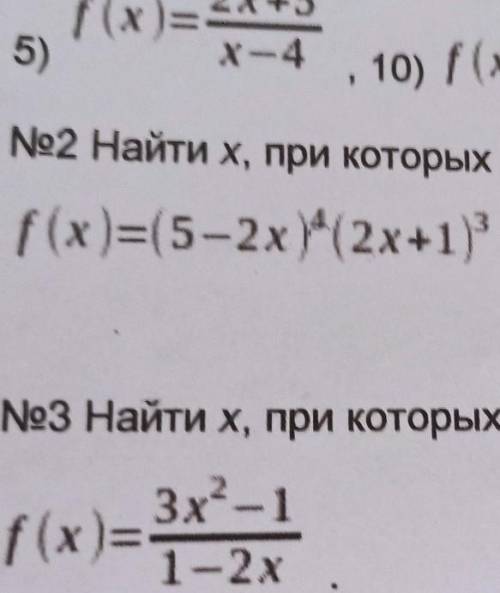
Другие вопросы по теме Математика
Популярные вопросы
- ИнформатикаВ 1 задана и x=17 z=4...
3 - Сұрақ Жауап 1 Спорт ненің кепілі ? 2 Жүгіруге кімнің рұқсаты керек ? 3 Спорт...
3 - Составьте диаграммы Льюиса, «точек и крестов», образования молекул следующих...
3 - Сочинение на тему: Превратности любви (желательно кратко)...
2 - Выполнить действия номер 1040...
2 - Рассказ о весне на французском 10 предложений...
3 - какая система земледелия была распространена на территории Беларуси в Раннем...
3 - Умножите дробь на целое число 26*5/78. 1)2,5 2)1 2/3 3)13/39 4)1 1/2...
1 - Кто мне перевести это на английский?...
1 - Что общего в рассказе чудик и в мульфильме Чудик?...
2
Чтобы найти значения x, при которых f'(x) = 0, мы должны приравнять это выражение к нулю и решить уравнение.
5 - 2x(2x + 1) = 0
Для решения данного уравнения, необходимо разложить скобки и привести подобные слагаемые:
5 - 4x^2 - 2x = 0
4x^2 + 2x - 5 = 0
Теперь, чтобы решить это квадратное уравнение, мы можем использовать формулу дискриминанта:
D = b^2 - 4ac
где a = 4, b = 2 и c = -5.
D = (2)^2 - 4(4)(-5)
D = 4 + 80
D = 84
После вычисления дискриминанта, мы можем найти значения x, используя формулу:
x = (-b ± √D) / 2a
x = (-2 ± √84) / (2 * 4)
x = (-2 ± √84) / 8
Таким образом, мы получаем два значения x:
x₁ = (-2 + √84) / 8
x₂ = (-2 - √84) / 8
Подробное решение уравнения может быть долгим и сложным, поэтому я рекомендую использовать калькулятор для вычисления значения корней.
Теперь перейдем к задаче №3, где нужно найти значения x, при которых f'(x) > 0. Функция f'(x) представлена в виде выражения 3x - 1.
Чтобы найти значения x, при которых f'(x) > 0, мы должны найти интервалы, на которых функция f'(x) положительна. Для этого мы должны решить неравенство:
3x - 1 > 0
Теперь решим это неравенство:
3x > 1
x > 1/3
Таким образом, значение x должно быть больше 1/3, чтобы функция f'(x) была положительной.
Надеюсь, что данное объяснение поможет тебе понять решение этих задач. Если у тебя возникнут дополнительные вопросы, не стесняйся задавать их.