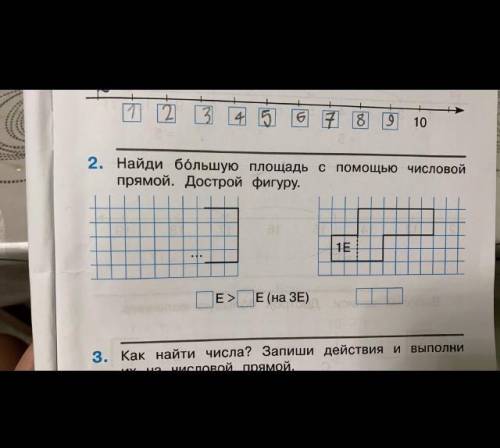
2. Найди большую площадь с числовой
прямой. Дострой фигуру.
1E
ПЕ> E(на ЗЕ)

Хорошо, я готов помочь вам с этой задачей. Давайте рассмотрим ее пошагово.

1. Дана числовая прямая и отрезок PE. Нам нужно найти большую площадь с числовой прямой и достроить фигуру.

2. Сначала найдем точку E на числовой прямой. Мы видим, что E должна находиться на правой стороне от P, так как есть знак ">", который указывает на больше. Поэтому мы отмечаем точку E справа от точки P на числовой прямой.

3. Теперь у нас есть отрезок PE на числовой прямой. Для построения фигуры, нам нужно соединить точки P и E линией. Мы рисуем линию от точки P к точке E и получаем треугольник PЕ.

4. Чтобы найти площадь этого треугольника, мы должны знать длины его сторон. Нам дана только числовая прямая, поэтому нам нужно определить длину стороны PE.

5. Если мы рассмотрим числовую прямую, мы видим, что точка Е находится правее точки P. Поэтому точка Е имеет большее значение, чем точка Р.

6. Для простоты предположим, что точка P имеет значение 1 на числовой прямой. Тогда, в соответствии с условием, точка E должна иметь значение больше 1. Давайте предположим, что она равна 3.

7. Теперь мы знаем, что отрезок PE равен 2 (3 - 1 = 2). Мы можем измерять длину в любых единицах, например в сантиметрах или дюймах, но в данном случае в условии не указано, поэтому давайте оставим его просто как 2.

8. Так как отрезок PE - это основание треугольника, а P - точка соединения основания с высотой, нам нужно знать высоту треугольника, чтобы вычислить его площадь.

9. В условии не указано, где находится высота треугольника относительно отрезка PE, поэтому давайте сделаем предположение, что она проходит через середину PE.

10. Итак, длина высоты треугольника равна половине длины основания. В нашем случае, длина высоты будет 1 (2 / 2 = 1).

11. Теперь мы знаем длину основания и высоты треугольника, поэтому мы можем вычислить его площадь. Площадь треугольника равна половине произведения длины основания и высоты: (2 * 1) / 2 = 2 / 2 = 1.

12. Таким образом, большая площадь с числовой прямой, образованная фигурой PЕ, равна 1.

Вот и ответ на вашу задачу. Если у вас возникнут какие-либо дополнительные вопросы, пожалуйста, не стесняйтесь задавать их.