2*9^(x)-3^(x+1)-9=0 решите показательное уравнение
Другие вопросы по теме Математика
Популярные вопросы
- Решить уравнение(x²-5x)+5-x=0...
2 - Гіпотенуза прямокутного трикутника АВ = 12, а катет АС = 8. Знайдіть радіускола...
1 - 1.Назовите признаки, которые могут свидетельствовать о приближении цунами...
1 - Какие команды нужно добавить вместо многоточия в программу для Черепахи: повтори...
2 - √y-x √2x-y ; зообразити графік нерівності даю 70б....
3 - Брусок pивномирно тянут по поверхности с горизонтальной силой 14 Н. Чему равен...
2 - Там сверху написано что делать...
3 - Заповніть пропуски у схемах реакцій, перетворіть їх на рівняння:а) H,SO4 +...
3 - Джерело звуку випромінює звукову хвилю частотою 15 кГц визначте швидкість...
1 - На стадионе игра: Футбольная школа Альфа - Футбольная школа Бета, счет матча...
2
1.
Пошаговое объяснение:
Пусть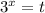 , t>0. Тогда уравнение принимает вид:
, t>0. Тогда уравнение принимает вид:
Так как t > 0, то t = 3.
Значит