1. Математика
  2. 1Обчисліть значення виразу

1Обчисліть значення виразу {cos}^{2} \frac{\pi}{12} - {sin}^{2} \frac{\pi}{12}

2Розв’яжіть рівняння:

А)

Б)

В)
.

3. Розв’яжіть нерівність
.

4. Чому дорівнює значення виразу 
, якщо
і

5. Спростіть вираз:

6. Дослідіть на парність функцію

​


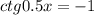
ctg0.5x = - 1
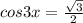
cos3x = \frac{ \sqrt{3} }{2}
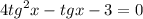
{4tg}^{2} x - tgx - 3 = 0
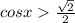
cosx \frac{ \sqrt{2} }{2}
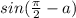
sin( \frac{\pi}{2} - a)
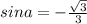
sina = - \frac{ \sqrt{3} }{3}
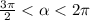
\frac{3\pi}{2} < \alpha < 2\pi
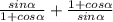
\frac{sin \alpha }{1+ cos \alpha } + \frac{1 + cos \alpha }{sin\alpha }
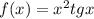
f(x) = {x}^{2} tgx

sochiru2014 sochiru2014    3   22.03.2021 16:21    0

Ответы
Показать ответы (3)
Другие вопросы по теме Математика
pozhidaevad pozhidaevad  17.08.2019 05:00
Вычисли.запиши ответ арабскими цифрами. d-l= xv+c= lxx-v= cxv-xxv=...
amir161 amir161  17.08.2019 05:00
Дано уравнение 20x2+47x−6=0. запиши старший коэффициент, второй коэффициент и свободный член....
tranatar tranatar  17.08.2019 05:00
При затруднении рассмотри такую запись 6454: 14=6454: {7*2]=6454: 7: 2=922: 2= закончи вычисления...
Face22821 Face22821  17.08.2019 05:00
Для учеников младших классов 286 завтраков для старшеклассников на 188 завтраков меньше сколько завтра кого предназначена ученика средних классов...
gjkbyf6789 gjkbyf6789  17.08.2019 05:00
Найди значения выражения (54/(-6)-24*(-5))/(-3)...
IvanWINNER IvanWINNER  17.08.2019 05:00
Волимпиаде учавствавало 54 человека . арифметическую решили 30 чел , - 10 чел , 5 и ту и другую , сколько человек решило : только арифметическую , только , не решило вообще...
BERE1337 BERE1337  17.08.2019 05:00
Сумма длин ребер прямоугольного параллелепипеда равна 28 см. найдите сумму длин трех его ребер, имеющих общую точку...
няшка366 няшка366  17.08.2019 05:00
Число 600 поделить на две части у видношени 5: 7...
Ррргчг2424 Ррргчг2424  17.08.2019 05:00
Разность чисел 70 и 75 увеличить в 5 раз сумму 43 и 30 увеличить на 5 разность чисел 30 и 10 уменьшить на 7 сумма чисел 20 и 15 уменьшить в 7 раз...
Geimer200 Geimer200  17.08.2019 05:00
Рассмотри рисунок составь и реши в которой спрашивается сколько всего книг взяли с полки...

Популярные вопросы