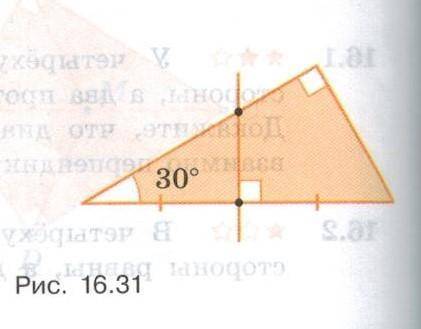
16.9 Острый угол прямоугольного треугольника равен 30°. На его гипотенузу опустили высоту. В каком отношении она её делит.

Добрый день! Давайте решим этот вопрос вместе.

У нас есть прямоугольный треугольник, в котором острый угол равен 30°. Мы знаем, что прямой угол в треугольнике равен 90°, поэтому есть еще один угол, который мы можем найти, используя свойство, что сумма углов треугольника равна 180°.

Давайте найдем этот угол:

Угол = 180° - (90° + 30°)
Угол = 180° - 120°
Угол = 60°

Теперь у нас есть все углы треугольника: 90°, 30° и 60°.

Мы знаем, что на гипотенузу треугольника опустили высоту. Итак, высота делит гипотенузу на две части. Давайте обозначим эти части с помощью букв: А и В.

Мы хотим найти, в каком отношении высота делит гипотенузу. Для этого нам поможет теорема Пифагора, которая говорит, что квадрат длины гипотенузы равен сумме квадратов длин катетов.

В нашем случае гипотенуза - это сторона, на которую опустили высоту, и она обозначается как С. Катетами будут стороны А и В.

Теорема Пифагора будет иметь такой вид:

С^2 = А^2 + В^2

Чтобы найти отношение, в котором высота делит гипотенузу, нам нужно найти соотношение между А и В.

Давайте для начала найдем С. Мы знаем, что два катета равны А и В. Исходя из этого, мы можем записать уравнение для С:

С = А + В

Теперь мы можем заменить С в теореме Пифагора:

(А + В)^2 = А^2 + В^2

Раскроем скобки:

А^2 + 2АВ + В^2 = А^2 + В^2

Заметим, что А^2 и В^2 сократятся:

2АВ = 0

В данном случае, мы получили, что произведение А и В равно 0. Это означает, что одно из них должно быть равно 0.

Если А равно 0, то высота делит гипотенузу в отношении 0:1, то есть она делит гипотенузу только на одну часть, и они равны.

Если В равно 0, то высота делит гипотенузу в отношении 1:0, то есть высота и гипотенуза совпадают.

В нашем случае, мы видим, что и А, и В не равны 0, поэтому мы приходим к выводу, что высота делит гипотенузу в отношении 1:1, то есть на равные части.

Итак, чтобы ответить на вопрос, высота делит гипотенузу на равные части. Я надеюсь, объяснение было понятным и информативным. Если у вас есть еще вопросы, не стесняйтесь задавать!