1. Математика
  2. 15 . на отрезок длиной

15 . на отрезок длиной 10см ставятся две точки. найти вероятность того, что из трёх получившихся частей можно составить треугольник. тема: определение вероятности. решать, используя омегу и тд.​

Ekaterina152005 Ekaterina152005    1   01.10.2019 22:14    6

Ответы
alina1427 alina1427  09.10.2020 10:30

Пусть x, y и 10 - x - y  — части отрезка. Тогда имеем ограничения

0\leq x\leq 10\\ 0\leq y\leq 10

x+y\leq 10

На рисунку у нас треугольник, ограниченный осями координат и прямой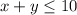 x+y\leq 10

По неравенству треугольника: сумма длин двух сторон не превышает третью сторону.

10-x-y\leq x+y~~~\Rightarrow~~~~ \boxed{x+y\geq5}

x\leq 10-x-y+y~~~~\Rightarrow~~~ \boxed{x\leq 5}\\ \\ y\leq10-x-y+x~~~\Rightarrow~~~ \boxed{y\leq 5}

Количество всевозможных исходов: площадь тр-ка ABC

n(\Omega)=\dfrac{10\cdot10}{2}=50

Площадь заштрихованного треугольника DEF:

S_{FED}=\dfrac{FE\cdot DE}{2}=\dfrac{5\cdot 5}{2}=\dfrac{25}{2} кв.ед.

n(A)=\dfrac{25}{2}

Искомая вероятность по формуле геометрической вероятности

P(A)=\dfrac{n(A)}{n(\Omega)}=\dfrac{25/2}{50}=\dfrac{1}{4}

ответ: 1/4.


15 . на отрезок длиной 10см ставятся две точки. найти вероятность того, что из трёх получившихся час
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
davleeva davleeva  30.04.2020 11:40
2. Определи аналитический зависимости, заданной табличным х12345у246810 1) y = 4x 2) y = x2 3) y = 4 + x 4) y = 2x 5) y = x + 10​...
никита3491 никита3491  30.04.2020 11:40
алгебра ребят, хелп, нужно решение...
burdick94 burdick94  30.04.2020 11:40
«Осевая и центральная симметрия»Вариант 11. Выберите верные утверждения:А. Квадрат имеет две оси симметрии.В. Равнобедренный треугольник имеет одну ось симметрин.С. Фигура...
булати булати  30.04.2020 11:40
Пользуйся графиком движения туристов к озеру ответь на во Сколько времени туристы шли к озеру? 2)Сколько всего км туристы? 3)Сколько времени туристы отдыхали у озера...
MegaFox06 MegaFox06  30.04.2020 11:40
Розчин містить 140 грам води через деякий час 50 г випаровали ,після чого концентрація солі збільшилась на 10%.Скільки грамів солі містить розчин...
aidarisiev80 aidarisiev80  30.04.2020 11:40
решить: Поезд 150 км всего пути проехал со скоростью 50 км/ч , вторую часть пути- 240 км со скоростью 60 км/ч, третью часть пути- 210 км со скоростью 70 км/ч. Чему равна...
Anutka87igorevna Anutka87igorevna  30.04.2020 11:40
Решите уравнение 9 (7 + x) -4x = 6x - 56​...
curtain curtain  30.04.2020 11:40
Выберите в каждом номере букву правильную ​...
evasaidova91 evasaidova91  30.04.2020 11:40
решить условие краткую запись не решение а краткую запись ​...
zbbzk zbbzk  30.04.2020 11:41
В каких четвертях координатной плоскости расположены точки, абсцисса которых равна -12, а ордината не равна 0? во II и в III четвертях в I и IV четвертях в I и во II четвертях...

Популярные вопросы