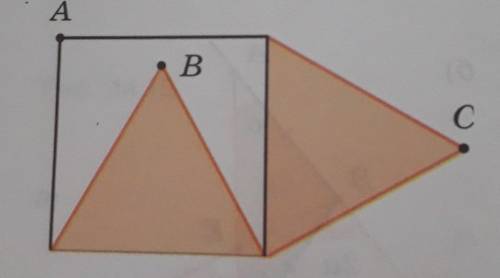
14.7 На двух сторонах квадрата построили рав-
носторонние треугольники так, как это показано
на рисунке 14.22. Лежат ли отмеченные на нём
точки A, B и C на одной прямой?​

Для решения данной задачи нам необходимо проверить, лежат ли точки A, B и C на одной прямой.

Для начала обратим внимание на то, что у нас имеется два равносторонних треугольника, которые построены на сторонах квадрата. Это означает, что все углы в этих треугольниках равны 60 градусам.

Посмотрим на треугольник ABC. Возьмем сторону AC. Обозначим величину этой стороны как а. Также обозначим стороны треугольника равностороннего треугольника, построенного на стороне квадрата, как b.

Поскольку у нас треугольник равносторонний, то все стороны равны друг другу. То есть, сторона AB также равна b.

Для проверки, лежат ли точки A, B и C на одной прямой, воспользуемся критерием коллинеарности трех точек. Если величина отрезка AC будет равна сумме величин отрезков AB и BC, то можно сделать вывод, что точки лежат на одной прямой.

Обозначим величину отрезка AC как с.

Согласно теореме Пифагора, для прямоугольного треугольника ABC (прямоугольник), гипотенуза AC можно выразить по теореме Пифагора:

AC^2 = AB^2 + BC^2

В нашем случае, точки A, B и C образуют прямоугольный треугольник ПОК. Таким образом, мы можем записать:

AC^2 = PK^2 + KO^2

AC^2 = a^2 + b^2

Теперь рассмотрим отрезок AB. Мы уже знаем, что AB = b.

Теперь рассмотрим отрезок BC. Он пройдет через центр квадрата и будет равен диагонали этого квадрата. Зная, что сторона квадрата равна b, мы можем применить теорему Пифагора, чтобы выразить длину диагонали:

BC^2 = b^2 + b^2

BC^2 = 2b^2

Теперь мы можем сравнить AC и сумму AB и BC:

a^2 + b^2 = b^2 + 2b^2

a^2 = 2b^2

Поскольку мы установили, что a^2 равно 2b^2, то можем утверждать, что величина отрезка AC равна сумме величин отрезков AB и BC. Следовательно, можно сделать вывод, что точки A, B и C лежат на одной прямой.