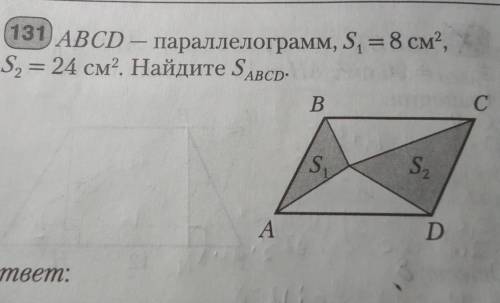
131) ABCD — параллелограмм, S1=8 см², S2= 24 см². Найдите S ABCD

Для решения этой задачи нам понадобятся знания о площади параллелограмма и свойствах параллелограмма.

1. Площадь параллелограмма вычисляется по формуле: S = a * h, где a - длина основания, h - высота, опущенная на основание.
2. Из свойств параллелограмма известно, что противоположные стороны равны и параллельны, и высота, опущенная на основание, является перпендикуляром к основанию и равна длине противоположной стороны.

Из условия задачи известно, что S1 = 8 см², S2 = 24 см². Нам нужно найти площадь параллелограмма S ABCD.

По формуле для площади параллелограмма:

S1 = a * h1,
S2 = a * h2,

где a - длина основания, h1 и h2 - высоты, опущенные на основание a.

Мы знаем, что противоположные стороны параллелограмма равны и параллельны. Обозначим длины основания и высоты как a и h соответственно.

Известные данные:
S1 = 8 см²,
S2 = 24 см².

Из свойств параллелограмма следует, что h1 = h2 = h (высоты равны).

Тогда уравнения для площадей S1 и S2 примут вид:

S1 = a * h,
8 = a * h,

S2 = a * h,
24 = a * h.

Разделим уравнения друг на друга, чтобы избавиться от переменной a:

S2 / S1 = (a * h) / (a * h),
24 / 8 = 3.

Таким образом, мы получили, что S2 / S1 = 3.

Поэтому площадь S2 равна трем S1.

Теперь мы можем найти площадь S ABCD.

S ABCD = S1 + S2.

Так как S2 = 3 * S1, заменим эту формулу в уравнении для S ABCD:

S ABCD = S1 + 3 * S1,
S ABCD = 4 * S1.

Теперь мы можем использовать значение S1, которое нам дано:

S ABCD = 4 * 8,
S ABCD = 32.

Ответ: Площадь параллелограмма ABCD равна 32 см².