#13 Найдите сумму всех целых n, где каждое из которых представляет сумма 16n+9 и 9n+16 является полным квадратом
A 29
B 53
C 37
D 42
Воздух5
1
31.01.2022 11:45
2
Другие вопросы по теме Математика
encl3
24.05.2019 03:30
azharik2k17
24.05.2019 03:30
tat321
24.05.2019 03:20
Eгор43
24.05.2019 03:20
steamoff
24.05.2019 03:20
kartofan2016p08uuy
24.05.2019 03:20
Ŕöömää999
24.05.2019 03:20
H1biki
24.05.2019 03:20
пргремм6
22.01.2021 12:07
Популярные вопросы
- Решить 2 целых 13/14 + 1 целая 20/21...
2 - Найдите координат точек пересечения графиков линейного уравнения - 3х+2х-6=0...
1 - С! ученик каменщика укладывает за 1 час x кирпичей, а каменщик за это...
3 - Составьте и запишите предложения с выделенными словами из стихотворения...
1 - Как готовились к встрече гостей в сказке черная курица...
2 - Упрямокутнику abcd кут bac=30°. з вершини d до діагоналі ac проведено...
1 - Вотымённых прилагательных пишется одна -н-?...
1 - 8. дівчинка дивиться у дзеркало, що висить на стіні підневеликим кутом...
2 - Текст: говорят: часы стоят, говорят: часы спешат, говорят: часы идут,...
3 - 2-тапсырма. сөйлемдегі көп нүктенің орнына керекті сөздерді (белгiсiздиесімдіктерін)...
2
Есл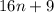и
и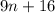 
одновременно полные квадраты, то их произведение -- тоже, а потому 
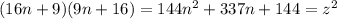. Однако 
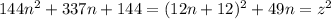, то есть 
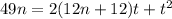. Легко видеть, что для 
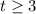решений уже нет. Потому остается проверить два случая: 
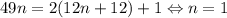и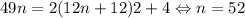 
. Они являются решениями. Их сумма -- 
.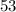