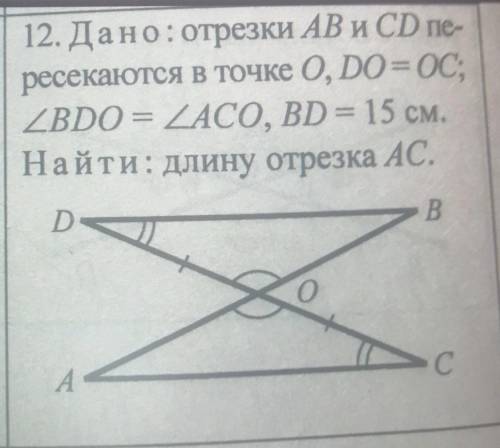
12. Дано: отрезки AB и CD пе- ресекаются в точке 0, D0= 0С; BD0 = ACO, BD = 15 см. Найти: длину отрезка АС.

Чтобы найти длину отрезка AC, нужно воспользоваться свойством подобных треугольников.

Дано, что отрезки AB и CD пересекаются в точке O, и известно, что D0 = 0С, BD0 = ACO и BD = 15 см.

Первым шагом мы можем заметить, что треугольник ABD и треугольник OCB подобны. Они имеют общий угол B и по теореме углового подобия, их соответствующие углы равны.

Далее, поскольку отрезок BD0 = ACO, мы можем сказать, что треугольник DBD0 и треугольник OCB также подобны.

Из подобия треугольников DBD0 и OCB, мы можем установить соотношение между сторонами:
BD0 / BC = BD / BO

Подставим известные значения:
ACO / BC = 15 / BO

Также, по теореме о треугольнике, сумма углов треугольника равна 180 градусов, поэтому можем сказать, что:
ACO + ABC + BOC = 180

Так как угол BOC = угол ABC, мы можем переписать это уравнение, заменяя угол BOC на x:
ACO + x + x = 180

ACO + 2x = 180

Итак, у нас получилось одно уравнение с одной неизвестной: ACO + 2x = 180.

Используем эту информацию для решения задачи:

1. Поскольку в треугольнике углы ACO и ABC имеют одну сторону AO, это значит, что ACO = ABC.
2. Также, из подобия треугольников DBD0 и OCB, мы можем сказать, что угол ABC = угол OCB = x.
3. Подставляем эти значения в уравнение ACO + 2x = 180: ACO + 2x = 180
ACO + x + x = 180
2x + x = 180
3x = 180
x = 60

Теперь, зная, что x = 60 градусов, мы можем найти значения оставшихся углов:
1. ACO = ABC = 60 градусов
2. BOC = 180 - ACO - ABC = 180 - 60 - 60 = 60 градусов

Таким образом, мы нашли все значения треугольника ADC.

Теперь, чтобы найти длину отрезка AC, мы можем использовать соотношение сторон подобных треугольников DBD0 и OCB:

ACO / BC = BD / BO

Подставляем значения:
60 / BC = 15 / BO

Дальше, мы знаем, что отрезки BD и BO образуют отрезок DO, который мы обозначили как BD0. Известно, что BD0 = ACO, это значит, что BD0 = 60.

Также, мы знаем, что DO = BD - BD0 = 15 - 60 = -45.

Теперь, мы можем использовать это знание в уравнении 60 / BC = 15 / BO:

60 / BC = 15 / (BO - DO)

Подставляем известные значения:
60 / BC = 15 / (BO - (-45))
60 / BC = 15 / (BO + 45)

Мы хотим найти BC, поэтому представим это уравнение в виде:
60 * (BO + 45) = 15 * BC

Раскроем скобки:
60BO + 2700 = 15BC

Делаем замену BO = x и BC = y:
60x + 2700 = 15y

Поделим это уравнение на 15, чтобы упростить его:
4x + 180 = y

Теперь мы можем представить y через x и решить это уравнение, чтобы найти значения x и y.

Вот, как решить уравнение:
4x + 180 = y

Так как мы хотим найти значения x и y, у нас есть два уравнения с двумя неизвестными:
ACO + 2x = 180
4x + 180 = y

1. Решим первое уравнение ACO + 2x = 180, где ACO = 60:
60 + 2x = 180
2x = 180 - 60
2x = 120
x = 60

2. Теперь, используя найденное значение x, мы можем решить второе уравнение 4x + 180 = y:
4 * 60 + 180 = y
240 + 180 = y
y = 420

Таким образом, мы нашли значения x = 60 и y = 420, которые соответствуют BO и BC соответственно.

Ответом на задачу является длина отрезка AC, которую мы искали.