100 ! ! исследовать на сходимость ряды 1) сума от 1 до бесконечности 1/(n^2 +2n +3) 2) сума от 1 до бесконечности sin(pi/2^n) 3) сума от 1 до бесконечности 1/(2n+1)!

ответ: 1) сходится 2) сходится 3) сходится

Пошаговое объяснение:

1) Известно, что ряд сумма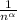 сходится при α > 1

В частности сходится и ряд суммы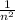

Т.к.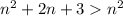

то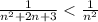

По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.

2) Аргумент синуса убывает от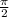 для 0

Следовательно рассматриваемый ряд положителен и для синуса можем записать

sinx < x

Исследуем на сходимость ряд сумм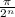

Найдем для него отношение последующего члена к предыдущему

По признаку Даламбера ряд сумм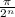 сходится.

По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами, т.е сходится и ряд сумм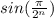

3. Найдем отношение последующего члена к предыдущему

При n стремящемся к бесконечности D стремится к нулю, а следовательно, по признаку Даламбера ряд сходится.