1. Математика
  2. 10 класс, ,(вариант 2). первое

10 класс, ,(вариант 2). первое я сделала, но боюсь, сама буду долго разбираться и возиться, завтра к/р

Саша11111111111уу Саша11111111111уу    2   02.04.2019 20:59    0

Ответы
999Человек999 999Человек999  28.05.2020 12:44

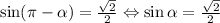2) \sin(\pi - \alpha) = \frac{\sqrt2}{2} \Leftrightarrow \sin \alpha = \frac{\sqrt2}{2} (1)

\cos 2\alpha = \cos^{2}\alpha - \sin^{2}\alpha = 1-2\sin^{2}\alpha

Используя (1) получаем:

\cos 2\alpha = 1-2\sin^{2}\alpha = 1-2\times(\frac{\sqrt2}{2})^{2} = 1-2\times \frac{1}{2}=0

Конечно, можно было найти значение угла и сразу его подставить, но я привел универсальное решение.

ответ: cos2α=0

3) а)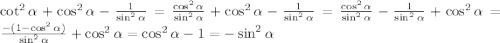\cot^{2}\alpha + \cos^{2}\alpha-\frac{1}{\sin^{2}\alpha} = \frac{\cos^{2}\alpha}{\sin^{2}\alpha}+\cos^{2}\alpha-\frac{1}{\sin^{2}\alpha} = \frac{\cos^{2}\alpha}{\sin^{2}\alpha}-\frac{1}{\sin^{2}\alpha}+\cos^{2}\alpha=\frac{-(1-\cos^{2}\alpha)}{\sin^{2}\alpha}+\cos^{2}\alpha = \cos^{2}\alpha - 1 = -\sin^{2}\alpha

Не забудь только cot(α) написать как ctg(α);

б)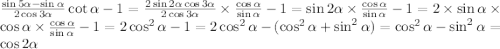 \frac{\sin5\alpha-\sin\alpha}{2\cos3\alpha} \cot\alpha-1 = \frac{2\sin2\alpha\cos3\alpha}{2\cos3\alpha}\times\frac{\cos\alpha}{\sin\alpha}-1=\sin2\alpha \times \frac{\cos\alpha}{\sin\alpha}-1=2\times \sin\alpha\times\cos\alpha\times\frac{\cos\alpha}{\sin\alpha}-1=2\cos^{2}\alpha-1 = 2\cos^{2}\alpha-(\cos^{2}\alpha+\sin^{2}\alpha)=\cos^{2}\alpha-\sin^{2}\alpha = \cos2\alpha

Тут тоже cot(α) поменяй на ctg(α);

Здесь была применена формула разности синусов:

\sin x - \sin y = 2\sin(\frac{x-y}{2})\cos(\frac{x+y}{2})

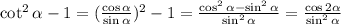4)\cot^{2}\alpha -1 = (\frac{\cos\alpha}{\sin\alpha})^{2}-1 = \frac{\cos^{2}\alpha-\sin^{2}\alpha}{\sin^{2}\alpha}=\frac{\cos2\alpha}{\sin^{2}\alpha}; И тут cot(α) ;)

5) a)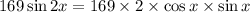 169\sin2x = 169\times 2\times \cos x \times \sin x

\sin x = \pm\sqrt{1-\cos^{2}x}=\pm\sqrt{1-\frac{25}{169} }=\pm\frac{12}{13}; Так как -π<x<0, то синус отрицателен. Подставим имеющиеся данные обратно в формулу:

169\sin2\alpha = 169\times 2\times (-\frac{5}{13})\times (-\frac{12}{13})=2\times 5\times 12=120

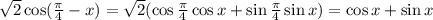
б) \sqrt2\cos(\frac{\pi}{4}-x) = \sqrt2 (\cos\frac{\pi}{4}\cos x + \sin\frac{\pi}{4}\sin x)=\cos x + \sin x

\sin x = \pm\sqrt{1-\cos^{2}x}=\pm\sqrt{1-\frac{9}{25} }=\pm\frac{4}{5}

Так как π≤x≤2π, то синус отрицателен. Подставим обратно:

\sqrt2 \cos(\frac{\pi}{4} -x) = \cos x+\sin x = -\frac{3}{5}-\frac{4}{5}=-\frac{7}{5}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
hihok hihok  05.06.2019 16:00
Раскройте скобки и подобные слагаемые -3*(2х-1)+2*(7+3х)...
жепа564 жепа564  05.06.2019 16:00
Сколько дм квадратных в 4 метрах квадратных...
irinatsotok7 irinatsotok7  05.06.2019 16:00
Заполните пропуски: 2кг 320г= ,2т 4ц= , 6275г = , 1т 5ц= ,326кг = ц кг, 2617г = кг г, 1275кг = т ц кг. 1267м = км м, 4мм = см мм....
Komar1006 Komar1006  05.06.2019 16:00
От москвы до владивостока 9104 км города уфа и красноярск расположены между москвой и владивостоком от москвы до красноярска 4031 км а от владивостока до уфы 7727 км сколько...
hdhdydjsh hdhdydjsh  05.06.2019 16:00
На лодочной станции было 120 лодок. двухместных лодок было 25% всех лодок.остальные лодки были четырёх местные. сколько было четырёхместных лодок...
1Маргарет1 1Маргарет1  05.06.2019 16:00
Вкомнате,длина которой 8 м,а ширина на 2 м меньше длины,надо по красить пол.сколько для этого понадобится краски, если по 150 г на 1м2...
bolatbekaliya bolatbekaliya  05.06.2019 16:00
Вычислите произведения: 3/5 * 5/6 6/7 * 7/6 9/10 * 40/27 17/23 * 46/51...
popygai2 popygai2  05.06.2019 16:00
От куска шёлковой ткани отрезали 6целых две-пятых метра,потом ещё 3целых три-десятых метра,после чего осталось 1целая одна-вторая метра.сколько всего метров шёлка было в куске?...
marusja82 marusja82  05.06.2019 16:00
Какие виды ран вы знаете ? и как их лечить ? мне срочь если были поставила хоть 100...
люда334 люда334  05.06.2019 16:00
Решить уравнение! 4x-15(2+3x)=7-24x...

Популярные вопросы