1. Математика
  2. 10(2x+1)^(4)-30(2x+1)^(2)-40

10(2x+1)^(4)-30(2x+1)^(2)-40 = 0 найти x, и объяснить как

Lumenarix Lumenarix    1   27.09.2019 01:20    0

Ответы
НаТаШаЯЯЯ НаТаШаЯЯЯ  08.10.2020 21:34

Поделим левую и правую части уравнения на 10(для удобства)

(2x+1)^4-3\cdot(2x+1)^2-4=0

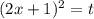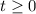Пусть (2x+1)^2=t, при этом t\geq 0 имеем квадратное уравнение относительно t:

t^2-3t-4=0

По теореме Виета:

t_1=-1 - не удовлетворяет условию при t ≥ 0

t_2=4


Обратная замена:

(2x+1)^2=4\\ (2x+1)^2-4=0

В левой части уравнения применим формулу разность квадратов

(2x+1+2)(2x+1-2)=0\\ (2x+3)(2x-1)=0

Произведение равно нулю, если хотя бы один из множителей обращается в нуль:

2x+3=0~~~\Rightarrow~~~ \boxed{x_1=-1.5}\\ 2x-1=0~~~\Rightarrow~~~ \boxed{x_2=0.5}


10(2x+1)^(4)-30(2x+1)^(2)-40 = 0 найти x, и объяснить как
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Altana020306 Altana020306  25.09.2019 14:00
Сколько будет 39 хв 18с -759 с . сколько ?...
Вайнесс Вайнесс  25.09.2019 14:00
Разложите на множители многочлен 6xy^2-18x...
Катерина26121 Катерина26121  25.09.2019 14:00
Два печенька сложили в печь за 16 часов известно, что первый из них, работая один, сложил бы печь за 24 часа. за сколько часов второй печник, сложил бы ту же печь....
Zaynab2897 Zaynab2897  25.09.2019 14:00
Велосипедист ехал по шоссе со скоростью 16 км ч остальное путь по проселочной дороге со скоростью 8 км ч весь путь составил 64 км сколько минут велосипедист затратил на путь по шоссе...
sie27 sie27  25.09.2019 14:00
Вмагазин 270 кг капусты. впервый день продали 120 кг. сколько частей капусты осталось продать во второй день?...
Gibertblite Gibertblite  25.09.2019 14:00
На острове невезения с населением 96 человек правительство решило провести 5 реформ .каждой реформой недовольна ровна половина всех граждан. гражданин выходит на митинг, если он недоволен...
vika26vf vika26vf  25.09.2019 14:00
Площадь прямоугольника равна 12 см². длины сторон прямоугольника равны a см и b см. найдите а, если b=2; 4; 6; 12. найдите формулу зависимости а от b. является ли эта зависимость обратно...
клэш4 клэш4  25.09.2019 14:00
Лодка двигаясь против течения за 2 часа, 4 часа км найдите собственную скорость лодки если скорость течения 2, 6 км ч...
som1712 som1712  25.09.2019 14:00
Паллада 720 кг овощей. моркови в 6 раз больше чем капусты, а лука -на 160 килограммов больше, чем капусты. сколько килограммов каждой культуры ?...
Karelina1988 Karelina1988  25.09.2019 14:00
Кто из народов живших на кубани готовил на праздник хортарике травяную еду ? большое !...

Популярные вопросы