10:(25-в^4) + 1:(5+в^2)-1:(5-в^2) больше 0,доказать
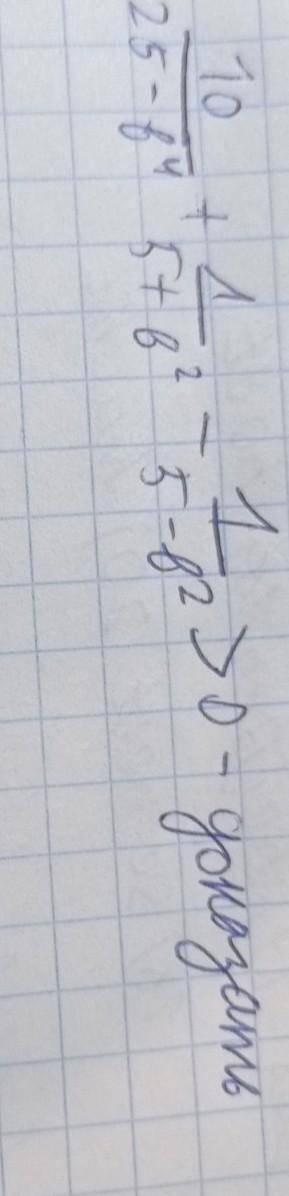
Другие вопросы по теме Математика
Популярные вопросы
- 1рисунок*нприсунке представлена схема определения жесткости пружины:...
1 - Сочинение по теме любви ревизор гоголь...
2 - P,05 + → h2po4 so, + koh → + mgo + → mg3(po4)2 + ligo + so, - .....
3 - 9. пуля движется с определенной скоростьи, попав в стенку, останавливается...
2 - Выпишите предложение, в котором нужно поставить одну запятую. (знаки...
2 - Что, по вашему мнению, произойдёт если маладежь перестанет заниматься...
1 - Сделайте из этого текста 6 краткий предложений для пересказ. каз...
3 - Найдите область определения функции....
1 - Какие направления внутренней политики были у карла 10, луи-филиппа...
3 - 1)какое значение имеют зелёные растения для живых организмов. 2)...
3
Пошаговое объяснение:
Пошаговое объяснение:
10/ (25-b⁴) + 1/ (5+ b²) - 1/ (5-b²) > 0 - доказать
Приведём дроби к общему знаменателю 25-b⁴, т.к.
25-b⁴ = (5+ b²) (5-b²)
10/ (25-b⁴) + 1/ (5+ b²) - 1/ (5-b²) =
= 10/ (25-b⁴) + 1(5-b²)/ (5+ b²)(5-b²) - 1(5+ b²)/ (5-b²)(5+ b²) =
= 10/ (25-b⁴) + (5-b²)/ (25-b⁴) - (5+ b²)/ (25-b⁴) =
= (10 + (5-b²) - (5+ b²))/ (25-b⁴) = (10 + 5-b² - 5- b²)/ (25-b⁴) =
= (10 -2b² ) / (25-b⁴) = 2(5-b²)/ (5-b²)(5+ b²) = 2/(5+ b²)
Рассмотрим дробь 2/(5+ b²). Дробь больше 0, когда её числитель и знаменатель одного знака. 2> 0, значит знаменатель тоже должен быть больше 0. Докажем, что
5+ b²>0,
b²> -5 (квадрат числа всегда больше 0 или равен 0), ч.и т.д.