1 задание производные 2 найти площадь криволинейной трапеции ограниченной
3 найти первообразные функции

1 задание производные 2 найти площадь криволинейной трапеции ограниченной 3 найти первообразные фун

Ответы

Lia20020313 24.07.2021 22:26

Пошаговое объяснение:

1) а) y = 2x^4 + 1/9*x^3 - 1/4*x^2 - 8x + 1

y ' = 8x^3 + 3/9*x^2 - 2/4*x - 8 = 8x^3 + 1/3*x^2 - 1/2*x - 8

б) y = x*cos x

y ' = 1*cos x + x(-sin x) = cos x - x*sin x

в)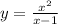 $y=\frac{x^2}{x-1}$

$y'=\frac{2x(x-1) - x^2*1}{(x-1)^2} =\frac{2x^2-2x-x^2}{(x-1)^2}=\frac{x^2-2x}{(x-1)^2}$

2) f(x) = x^2; a = 3; b = 4

$S = \int\limits^4_3 {x^2} \, dx = \frac{x^3}{3} |^4_3 = \frac{4^3}{3} - \frac{3^3}{3} =\frac{64}{3} -\frac{27}{3} = \frac{37}{3} = 12 \frac{1}{3}$

3) y = x^5 + 2x

$F(x) = \int {(x^5 + 2x)} \, dx =\frac{x^6}{6} + x^2 + C$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

mariuaivanova1 18.07.2019 20:50

Камилла1004 18.07.2019 20:50

HiDolr 18.07.2019 20:50

LeylaAllesgerova 18.07.2019 20:50

Маша07122005 18.07.2019 20:50

mirapax1997ozb3lk 18.07.2019 20:50

Все о церковных православных храмах...

akovlevavika444 18.07.2019 20:50

Реши уравнения,412: х=2 х*3=1009-682...

Shady2002 18.07.2019 20:50

Установите равны ли дроби 12/15 и 2/15...

gafman 18.07.2019 20:50

Кatе 18.07.2019 20:50