1 задание  
1 вариант

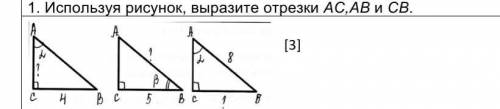
1. Используя рисунок, выразите отрезки AС,АВ и СВ.
1. Используя рисунок, выразите отрезки АС, СВи ВА.
 [3]
 
 
2. Две стороны прямоугольного треугольника равны: 6 см и 8 см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи.                           [4]
2. Две стороны прямоугольного треугольника равны: 3 см и 5 см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи.                  [4]
3. Известно, что =. Найдите значение остальных тригонометрических функций  [3]
3. Известно, что . Найдите значение остальных тригонометрических функций
[3]

 
4. Упростите выражение [5]
5. Дан прямоугольный треугольник,  с=25см b=7 см. Найдите неизвестные  элементы треугольника                            [3] 
5.Дан прямоугольный треугольник,  a=8см , b=15см. Найдите неизвестные  элементы треугольника     .[3] 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
​

1. Используя рисунок, выразите отрезки АС, СВ и ВА:
- Отрезок АС - это отрезок соединяющий точки А и С. По рисунку видно, что А и С находятся на одной прямой и не имеют других точек между собой, значит АС - это сам отрезок, обозначенный этой прямой.
- Отрезок СВ - это отрезок соединяющий точки С и В. По рисунку видно, что С и В находятся на одной прямой и не имеют других точек между собой, значит СВ - это сам отрезок, обозначенный этой прямой.
- Отрезок ВА - это отрезок соединяющий точки В и А. По рисунку видно, что В и А находятся на одной прямой и не имеют других точек между собой, значит ВА - это сам отрезок, обозначенный этой прямой.

2. Две стороны прямоугольного треугольника равны: 6 см и 8 см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи:
Мы знаем, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы по теореме Пифагора. В данном случае у нас есть два катета, длины которых равны 6 см и 8 см. Используя теорему Пифагора, мы можем найти длину гипотенузы с помощью следующей формулы:

гипотенуза^2 = катет1^2 + катет2^2

1) Заменяем значения катетов в формуле:
гипотенуза^2 = 6^2 + 8^2
гипотенуза^2 = 36 + 64
гипотенуза^2 = 100
гипотенуза = √100
гипотенуза = 10 см

Таким образом, третья сторона треугольника равна 10 см.

3. Известно, что . Найдите значение остальных тригонометрических функций:
Мы знаем, что тангенс равен отношению противолежащего катета к прилежащему катету:
тангенс = .

1) Определяем противолежащий катет и прилежащий катет по данному углу. По рисунку видно, что противолежащий катет - это отрезок синуса, а прилежащий катет - это отрезок косинуса.
2) Подставляем значения отрезков в формулу:
тангенс = .
тангенс = = = 1.

Таким образом, тангенс угла равен 1.

4. Упростите выражение:
Для упрощения выражения нам необходимо выполнить в нем арифметические операции:
3 * (4 + 5) - 6 * 2
Сначала выполняем операции в скобках:
3 * 9 - 6 * 2
Затем выполняем умножение:
27 - 12
И, наконец, выполняем вычитание:
15

Таким образом, результат упрощенного выражения равен 15.

5. Дан прямоугольный треугольник, с=25 см, b=7 см. Найдите неизвестные элементы треугольника:
Мы знаем, что в прямоугольном треугольнике гипотенуза равна корню из суммы квадратов катетов по теореме Пифагора. В данном случае у нас известны два катета, длины которых равны 7 см и 25 см. Мы можем найти гипотенузу с помощью следующей формулы:

гипотенуза^2 = катет1^2 + катет2^2

1) Заменяем значения катетов в формуле:
гипотенуза^2 = 7^2 + 25^2
гипотенуза^2 = 49 + 625
гипотенуза^2 = 674
гипотенуза = √674
гипотенуза ≈ 25,98 см

Таким образом, длина гипотенузы примерно равна 25,98 см.

Остальные элементы треугольника, такие как углы и площадь, могут быть найдены с использованием других формул и соотношений в геометрии. В задании они не указаны.