1) выразить log30 8 через а и b, если а=lg 5, b=lg 3. 2) выразить log350 140 через m и n, если m= log5 2, n=log7 5
Другие вопросы по теме Математика
Популярные вопросы
- Приведи дроби 6t/x+t и 12x/−x−t к общему знаменателю....
3 - Решите линейное уравнение:1/6y=1/3действия прописать...
3 - 3. Рассмотрите инфографику, Расскажите, които организации культуры судоструют...
1 - 1.Укажите факторы природной и социальной среды. 2.Как возникла социальная среда...
2 - Составь 3 предложение о путешествие с водными словами...
3 - АЙТЫЛЫМ 6 тапсырма. Сұрақтарға жауап бер....
1 - 145 | Прочитайте. Определите, в каком ряду во всех словах на месте пропуска пишется...
2 - История Гаара))) СабакуНо Гаара...
1 - Сообщение о творчестве драматурга бернарда шоу и его пьесе пигмалион...
1 - допиши конец мифа Дедал и икар...
1
1)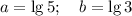
=================================
======================================
Использованы формулы