1. Вычислите cosa, tga, ctga, если sina = -15/17 и π < a < 3π/2 2. Упростите выражение:
(sin a + cos a)^2 - 2 sin a * cos a =
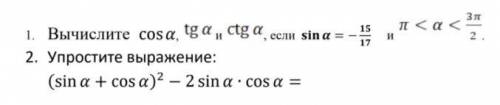
Другие вопросы по теме Математика
Популярные вопросы
- Скорость реакций творческая работа аналитическая творческая...
3 - А) грачиная скороговорка. грачиха говорит грачу: слетай с грачатами к врачу....
2 - A) отгадать загадки. 1)меня ждут не дождутся, а как увидят-разбугутся. 2)что...
1 - 20 на каком художественном приеме построенно стихотворение? знаменитый акробат...
3 - На чём основывалась османская империя? ? надо на кр...
2 - Счтению разделите текст сказка о жабе и розе и составьте план...
3 - Длинна 5м. ширина 4/5 от длинны. высота 3/4 от ширины...
3 - Что такое ямк? кто предложил такую систему?...
3 - Как нужно определять какой артикль вставлять a or an,the?...
1 - Сочинение - эссе на тему должны ли туристы соблюдать обычаи стран которые они...
1
1. Чтобы вычислить значения функций тригонометрии (cos a, tg a, ctg a), нам необходимо знать значение sin a. У нас дано, что sin a = -15/17, и дополнительно известно, что π < a < 3π/2.
Для начала, определим значение cos a. Используем известную формулу, связывающую sin a и cos a:
sin^2 a + cos^2 a = 1
Заменив sin a на -15/17, получаем:
(-15/17)^2 + cos^2 a = 1
Упростим это уравнение:
225/289 + cos^2 a = 1
cos^2 a = 1 - 225/289
cos^2 a = (289 - 225)/289
cos^2 a = 64/289
Так как π < a < 3π/2, то cos a < 0. Извлечем корень из полученной дроби:
cos a = -√(64/289)
cos a = -8/17
Теперь можно перейти к нахождению tg a и ctg a.
tg a = sin a / cos a = (-15/17) / (-8/17) = 15/8
ctg a = cos a / sin a = (-8/17) / (-15/17) = 8/15
Итак, получили значения:
cos a = -8/17
tg a = 15/8
ctg a = 8/15
2. Упростим выражение (sin a + cos a)^2 - 2 sin a * cos a. Для этого воспользуемся формулой (a + b)^2 = a^2 + 2ab + b^2:
(sin a + cos a)^2 - 2 sin a * cos a = sin^2 a + 2sin a * cos a + cos^2 a - 2 sin a * cos a
Удалим слагаемые, в которых участвуют sin a * cos a:
sin^2 a + cos^2 a
Так как по основному тригонометрическому тождеству sin^2 a + cos^2 a = 1, получаем:
(sin a + cos a)^2 - 2 sin a * cos a = 1
Надеюсь, я ответил на ваш вопрос подробно и понятно. Если у вас еще возникнут вопросы, не стесняйтесь задавать!