1. Математика
  2. 1. вычислить значение производной

1. вычислить значение производной функции заданной неявно
3x-2y+z=xz+5 в точке m_{0} (0,1,-1)
2. исследовать функцию z= 2xy-3x^2-2y^2+10 на
экстремумы

freks2 freks2    2   29.08.2019 12:12    18

Ответы
meowpeww10 meowpeww10  06.10.2020 02:52

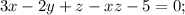
1.3x-2y+z-xz-5=0;

F(x,y,z)=3x-2y+z-xz-5;

$\frac{\partial F}{\partial x}=3-z; \frac{\partial F}{\partial y}=-2; \frac{\partial F}{\partial z}=1-x

$z'_x=\frac{F'_x}{F'_z}=\frac{3-z}{1-x}; z'_y=\frac{F'_y}{F'_z}=\frac{-2}{1-x}; z'_x=\frac{3+1}{1}=3; z'_y=\frac{-2}{1}=-2

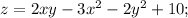
2. z=2xy-3x^2-2y^2+10;

z'_x=2y-6x; z'_y=2x-4y

$\left \{ {{z'_x=0} \atop {z'_y=0}} \right. \Rightarrow \left \{ {{2y-6x=0} \atop {2x-4y=0}} \right.; \left \{ {{2y=6x} \atop {2x-12x=0}} \right.; \left \{ {{x=0} \atop {y=0}} \right.

Чтобы определить, является ли точка (0;0) экстремумом , считаем вторые производные

z'_{xx}=-6; z'_{xy}=2; z'_{yy}=-4;

И смотрим выполнение достаточного условия экстремума

\begin{vmatrix}z'_{xx} & z'_{xy}\\ z'_{xy} & z'_{yy}\end{vmatrix}

Считаем это:

z'_{xx}z'_{yy}-2z'_{xy}=(-6)\cdot (-4) - 2\cdot2=24-4=200

Значит, точка (0;0) является экстремумом.

Так как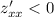 z'_{xx}, то точка (0;0) - максимум.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
pavelakur pavelakur  06.07.2019 15:40
Вычисли значения выражения (40-20)+15=...
Lena89269295717 Lena89269295717  06.07.2019 15:40
Катер,имеющий собственную скорость 15,5 км/ч,проплыл 2 часа по течению и 3 часа против течения,скорость течения реки равна 2км/ч. чему равно расстояние,которое проплывет...
vikysik927 vikysik927  06.07.2019 15:40
Вставь пропущеные числа (единицы полощади) 50 000мм2=_см2 6000м2= а _мм2=50дм2 _м2=6 км2 200000 м2= га 690000 а= км2 30000 см2= дм2 500 км2= га 4 а= м2 20м2= см2 12...
semic1 semic1  06.07.2019 15:40
Расстояние между посёлками к и т 50 км из двух посёлков в противоположных направлениях выехали 2 автомобиля один проехал 18 км а другой 17 км на каком расстояние друг...
alishraup alishraup  06.07.2019 15:40
Мне! ) разделите число 8.05 на две части так чтобы 75% одной из них были равны 40% другой...
shyndari shyndari  06.07.2019 15:40
Запишите в порядке возрастания числа 2,6; 2,09; 2,606; можете рассписать подробно заранее прибольшое...
Chelovechena1 Chelovechena1  06.07.2019 15:40
5класс . асыцыацыя уровнения рисунок ?...
Полюшенцыя Полюшенцыя  06.07.2019 15:40
Решите уравнение 5в+4в+в=720 и выберите верный вариант ответа: a) в=8; b) в=72; c) в=80....
bachko2012 bachko2012  06.07.2019 15:40
50ед = ? дес 365ед=? дес ? ед 2120ед=? сот дес 5050ед=? тыс ? ед 100мм=? см 184=? м ? дм 184дм=? м ? дм 1190=? м ? дм 9006м=? км ? м...
nomerperv nomerperv  06.07.2019 15:40
*6+576: *24: 42+66))*35+345)-28*17 решите а...

Популярные вопросы