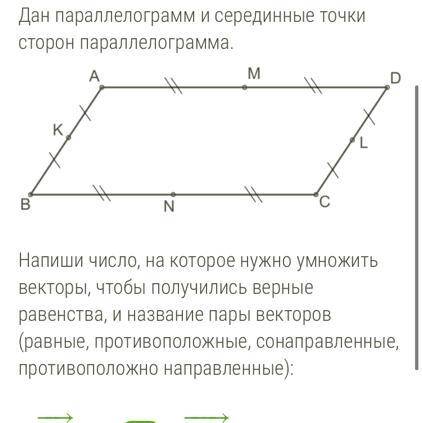
1) вектор DC= … • вектор NM, эти векторы …. 2) вектор NM = … • вектор BK, эти векторы …
3) вектор MD = … • вектор AD, эти векторы …
4) вектор AD = … • вектор CN, эти векторы …
На месте … нужно вписать ответы

1) вектор DC = -1 • вектор NM, эти векторы коллинеарны (сонаправлены в противоположные стороны).

Обоснование: Вектор DC можно представить как разность координат точек D и C, то есть DC = CD = (x_D - x_C, y_D - y_C). Вектор NM можно представить как разность координат точек N и M, то есть NM = MN = (x_N - x_M, y_N - y_M). Подставим координаты точек в формулу и получим: DC = (x_D - x_C, y_D - y_C) = (-x_C + x_D, -y_C + y_D) = -1 • (x_N - x_M, y_N - y_M) = -1 • NM. Таким образом, вектор DC равен -1, умноженному на вектор NM, значит эти векторы коллинеарны.

2) вектор NM = 1 • вектор BK, эти векторы пропорциональны.

Обоснование: Вектор NM можно представить как разность координат точек N и M, то есть NM = MN = (x_N - x_M, y_N - y_M). Вектор BK можно представить как разность координат точек B и K, то есть BK = KB = (x_B - x_K, y_B - y_K). Подставим координаты точек в формулу и получим: NM = (x_N - x_M, y_N - y_M) = 1 • (x_B - x_K, y_B - y_K) = 1 • BK. Таким образом, вектор NM равен 1, умноженному на вектор BK, значит эти векторы пропорциональны.

3) вектор MD = 2 • вектор AD, эти векторы коллинеарны (сонаправлены).

Обоснование: Вектор MD можно представить как разность координат точек M и D, то есть MD = DM = (x_M - x_D, y_M - y_D). Вектор AD можно представить как разность координат точек A и D, то есть AD = DA = (x_A - x_D, y_A - y_D). Подставим координаты точек в формулу и получим: MD = (x_M - x_D, y_M - y_D) = 2 • (x_A - x_D, y_A - y_D) = 2 • AD. Таким образом, вектор MD равен 2, умноженному на вектор AD, значит эти векторы коллинеарны.

4) вектор AD = -2 • вектор CN, эти векторы коллинеарны (сонаправлены в противоположные стороны).

Обоснование: Вектор AD можно представить как разность координат точек A и D, то есть AD = DA = (x_A - x_D, y_A - y_D). Вектор CN можно представить как разность координат точек C и N, то есть CN = NC = (x_C - x_N, y_C - y_N). Подставим координаты точек в формулу и получим: AD = (x_A - x_D, y_A - y_D) = -2 • (x_C - x_N, y_C - y_N) = -2 • CN. Таким образом, вектор AD равен -2, умноженному на вектор CN, значит эти векторы коллинеарны.