1. у=1/корень 4-х^2 найти д (у)
2.у= х/х+2 + 4/х-3 найти д (у)
3. у= 1/2 х+3 убывает или возрастает и точки экстрим если есть
4.у= -х^2 +4 убывает или возрастает и точки экстрим если есть
Другие вопросы по теме Математика
Популярные вопросы
- Накресли видризок k m задовжки 12 см и подили його на 6 ривних частин?...
3 - Складіть будь ласка питальне речення на ці слова : 1. відбирати 2. телеграма. 3....
1 - Як правильно написати : похмурої осіні\осені...
2 - Напиши что означают эти слова: полис,ареопаг,демос....
3 - Из 12 кг металла получается 8 деталей.сколько килограммов металла потребуется для...
1 - Длина окружности 25.12 найдите радиус трёх восьмых...
2 - Как сравнивать инструменты художник и инструменты с редактора pain...
3 - Стороны прямоугольника пропорциональны числам 3: 4,а его площадь 48 см.определите...
1 - Какие человеческие пороки высмеивает крылов в баснях осёл и соловей , ларчик ,...
3 - Мини сочинение на тему моя четырёх комнатная квартира...
2
1.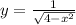
D(y): 4-x²>0 ⇔ (2-x)·(2+x)>0
Определим знак (2-x)·(2+x):
+ · - = - + · + = + - · + = -
-∞ --------[-100]-------(-2)------[0]------(2)-----[100]------> +∞
D(y)=(-2; 2)
2.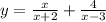
D(y): x+2≠0 и x-3≠0 ⇔ x≠-2 и x≠3
D(y)=(-∞; -2) ∪ (-2; 3) ∪ (3; +∞)
3.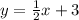
Значит, функция монотонно возрастает и поэтому точек экстремума нет.
4. y= -x²+4
y'= (-x²+4)'= (-x²)'+(4)'= -2·x+0= -2·x
y'(x)= 0 ⇔ -2·x=0 ⇒ x = 0
Для x < 0
y'(x)= -2·x >0, то есть для x∈(-∞; 0) функция монотонно возрастает,
а для x > 0
y'(x)= -2·x <0, то есть для x∈(0; +∞) функция монотонно убывает.
Тогда x = 0 является точкой максимума, то есть точкой экстремума.