1) сравните числа и результат запишите в виде неравенства и) -2/15 и 3/4 к) -3/4 и -4/5; -2 2/7 и 3 3/7 л) -7/10 и -3/8 2)Приняв за единичный отрезок длину 6 клеток тетради, начертите координатную прямую и отметьте на ней точни K(1/3; C(-0.5); d(-1 1/3); e(1/6) f(1 1/6) A(-5/6) B(2/3 R(-1/6) M(1.5)
Другие вопросы по теме Математика
Популярные вопросы
- Четырех угольник abcd вписан в окружность. угол abc равен 125,угол...
3 - 4x^2*y-x^3-4xy^2 представьте в виде произведения выражение...
3 - Как чаще всего зимой встречаются птицы – поодиночке или стаями?...
2 - Познакомься с информацией из толкового словаря объект,субьект.выбери...
2 - Выпишите числительные: двое пашут, а семеро руками машут. семерым...
1 - Вставить a/the 1.this radio. 2.i .3.this my friend lulu. 4.mummy...
3 - Государство составить предложение которые есть все члены предложение...
1 - Что является лишним в ряду и почему: битва за москву, сталинградская...
1 - Верное утверждение о реках россии! а)река ангара-приток оби б)река...
2 - 2х-3)(2х+3)=(х-1)(х+1)+(5х+2)(х-14)...
2
1. и)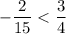 ; к)
; к) 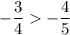 ;
; 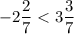 ; л)
; л) 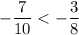
2. Точки построены. См. рисунок.
Пошаговое объяснение:
Требуется сравнить числа и записать их в виде неравенства. Также, приняв за единичный отрезок длину 6 клеток тетради, начертить координатную прямую и отметить на ней точки.
1. Сравним числа:
и)
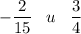
Отрицательное число всегда меньше положительного.к)
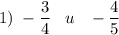
Чтобы сравнить две дроби с разными знаменателями, надо вначале привести их к общему положительному знаменателю, а затем сравнить.Используем основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, получим дробь, равную данной.Приведем дроби к общему знаменателю 20:
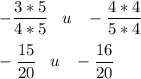
Из двух отрицательных чисел больше то, у которого модуль меньше.Также вспомним:
Модуль положительного числа - само число, а модуль отрицательного - число, противоположное данному.Сравним модули чисел:
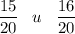
Из двух дробей с общим положительным знаменателем больше та, у которой больше числитель.Следовательно:
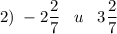
Отрицательное число всегда меньше положительного.л)
Приведем дроби к общему знаменателю 40, пользуясь основным свойством дроби:
Сравним модули этих дробей:
Следовательно:
2. Начертим числовую ось и отметим единичный отрезок 6 клеток.
Если наш единичный отрезок 6 клеток, то одна клеточка будет равна одной шестой части.
Воспользуемся основным свойством дроби.
Данные дроби, у которых знаменатель отличный от 6, приведем к знаменателю 6.
Затем отметим эти числа на числовой оси.
Отметим точки на числовой оси: