1+sin2x=2sinx+cosx решите уравнение
Другие вопросы по теме Математика
Популярные вопросы
- Лист від імені літературного героя...
3 - Выберите правильные ответы. Что должно быть в сжатом изложении? а Дополнительная...
2 - Измерьте углы SOK и SOM , изображенные на рисунке. Вычислите градусную меру угла...
1 - Подумай и впиши опорные слова для высказывания о том, где можно найти информацию...
1 - Жазылым Батыр туса ел ырысы такырыбын эссе туринде талкыланыз. Жазылымда одагай...
3 - 1. Денені шынықтырудың қандай пайдасы бар? Дұрысынсары түспен боя.Спортшы боласыңСергек...
3 - В процессе сушки яблоки теряют 60% своей массы. Сколько килограммов свежих яблок...
1 - решить♥️ Ничего не понимаю:( Заранее...
2 - Среди приведенных формул выберите те, которые отвечают веществам с ионной связью...
3 - Частку Не треба писати ОКРЕМО з наступним словом у рядку 1) не/має лиця на ньому...
2
Відповідь:
Покрокове пояснення:
n ∈ Z;
n ∈ Z;
Відповідь: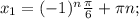 n ∈ Z;
n ∈ Z;