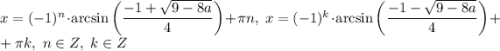1) sin^2x + sinx + a = 0 (параметр)
2) cos2x - sinx =a (параметр)
при всех значениях "а" развязать уравнение.
Другие вопросы по теме Математика
Популярные вопросы
- По дорожке бассейном плавают с постоянным не одинаковыми скоростями 2 спортсмена....
1 - Справа, слева, самосвал, землеройка, страна, лампа, налево, направо, молоко, снегоход...
1 - Скільки разів перейменовували луганськ?...
1 - 10. бабушка приготовила два блюда, миша идет сесть побольше того идругого и при...
1 - Сложное предложение с различными связи....
2 - Какой кинетической энергией обладает велосипещист , масса которого вместе с велосипедом...
3 - Что такое фонетические близнецы в правописании приставок пре- при- и есть ли правило...
1 - Висота прямокутної трапеції , проведена з вершини тупого кута, поділяє її основу...
1 - Письмо you have received a letter from your english-speaking pen friend barry. i...
1 - Сосуд объёмом 458 см3 наполнен 370,98 г жидкости. плотность жидкости равна округли...
1
Замена: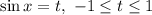
Данное уравнение будет иметь корни, если , то есть
, то есть 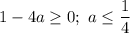
Имея два действительных корня, определим, при каких выполняется неравенство
выполняется неравенство 
Учитывая , имеем:
, имеем: ![a \in \bigg[-2; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/1ef46.png)
Учитывая , имеем:
, имеем: ![a \in \bigg[0; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/d8d0e.png)
Обратная замена:
ответ: если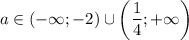 , то уравнение не имеет корней; если
, то уравнение не имеет корней; если 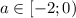 , то
, то 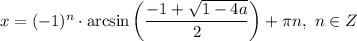 ; если
; если ![a \in \bigg[0; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/d8d0e.png) , то
, то 
Решаем аналогично:
Замена: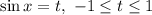
Учитывая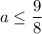 , имеем:
, имеем: ![a \in \bigg[-2; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/856ab.png)
Учитывая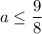 , имеем:
, имеем: ![a \in \bigg[0; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/76212.png)
Обратная замена:
ответ: если , то уравнение не имеет корней; если
, то уравнение не имеет корней; если 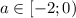 , то
, то 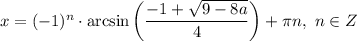 ; если
; если ![a \in \bigg[0; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/76212.png) , то
, то